Ìàòåìàòèêà/3. Òåîðèÿ âåðîÿòíîñòåé è

ìàòåìàòè÷åñêàÿ ñòàòèñòèêà

 

Burakovski V.

F. Skorina Gomel State University, Belarus

 

SOME RESULTS FOR MULTITOKEN RING LOCAL

AREA  NETWORKS

 

         Nonsymmetric and symmetric multitoken ring local area networks LAN with   stations in which each station has  finite capacity buffer is studied. The message arrival streams at each station are assumed to be  independent Poisson processes with arrival rate   for the -th station, , for nonsymmetric and  for symmetric ring. We consider the gated service discipline at each station. The stationary probabilities of considered local area networks and main characteristics were obtained.

         Keywords: multitoken ring network, gated service discipline, stationary probabilities.

 

1. INTRODUCTION

         One of the most effective schemes in a ring data-communication networks is token-passing [1,2,3]. Multitoken ring local area networks give an opportunity for some stations to transmit messages at the same time. In these networks there are finite number of tokens circulating cyclicly among the stations so that arriving messages can be transmitted from the definite stations simultaneously.

         In this paper we propose the multitoken LAN protocol. The proposed approach

is based on the idea that there are  tokens circulate in network. The arrival and departure moments for all tokens are assumed to be synchronized for all stations. Each station has finite capacity  buffer for the arrived messages. The gated service discipline gives an opportunity for the busy station to transmit all messages from it's buffer at the moment token arrives.

 

2. NONSYMMETRIC MULTITOKEN RING LAN

         We consider nonsymmetric token-passing ring local area network with  stations. Each station has a finite capacity  buffer. The walk time for any token to move from one station to the next one is assumed to be a constant equal to  (it depends on the speed of backbone). The service time for one message for any station is ( is the time for copping message at the station). The message arrival streams at each station are assumed to be independent Poisson processes with arrival rate  for the -th station, .

         We consider the gated service discipline, which assumes that the station transmits all messages from the buffer when the token arrives.

         The buffer at the station is blocked during the transmission time from all

stations and token is at the station.

         Let us denote by  the state  of the multitoken ring LAN, where -is the  number of the station where token arrives, , and  is the number of customers at the -th station, , at the moment when tokens arrive at correspondent stations, . The steady-state probabilities vector is denoted by .

         The behavior of considered LAN at the moments when tokens arrive at the stations can be described with the help of periodical Markov chain. Let us denote by matrix of the transition probabilities, where  are  the numbers of the stations where tokens arrive. It is evident that the numbers of the next stations where tokens come are .

         The steady-state probabilities of considered LAN are the solution of the

following matrix-vector system:

 

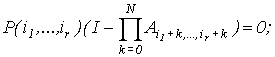
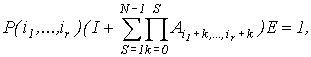
where  is vector of  units,  is  unit matrix.

         Complex formula for the transition probabilities also was obtained.

         The  definition of the main characteristics of the LAN is based on the steady-state probabilities.

 

3. SYMMETRIC MULTITOKEN RING LAN

 

         The symmetric ring LAN with  stations and  tokens is considered. Buffer capacity at each station is . We assume that service discipline is gated and at the moment token comes all customers pack in one  packet. Their service time is . The message arrival streams are independent Poisson with rate  for each station.

         We denote by , the steady-state probabilities where  is a number of customers in the queue at the station. We can define these probabilities from the system

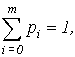
where  is  – matrix of transition probabilities, which we can obtain with the  help of formulas:

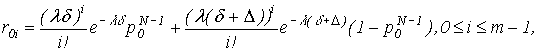
         We have obtained the main characteristics of this LAN [4,5,6,7] . It is interesting to investigate LAN with -limited and Bernoulli service disciplines.

 

 

         References

1.     ANSI/IEEE 802.5 Standard-1985. Token-passing ring access method and physical layer specification // IEEE Press, 1985. – 89 p.

2.     Martini P., Welzel T. The analysis of a token ring backbone // IEEE INFOCOM'88: Conf.Comput.Commun.:Proc. 7th Annu.Joint.Conf., New Orleans, LA, March 27-31, 1988: Networks: Evol: Revol? – P.467-476.

3.      Takagi H. Analysis of polling systems. Cambridge: Mit Press,1986. – 198 p.

4.      Burakovski V.V. Symmetric multitoken ring local area networks // Aerospace apparatus  construction of Russia. Series 2. S.-Pb., NAAP, 2005. Vol.4. P.117-122.

5.      Burakovski V.V., Rodchenko V.O. Local area networks // Gomel, F.Skorina GSU, 2008. – 78 p.

6.      Burakovski V.V., Rogachev A.A. Multitoken ring local area network with finite buffers and ordinary service // New mathematical methods and computer technologies in design,  industry and scientific investigations. Gomel, F.Skorina GSU, 2003. – P.127-128.

7.      Burakovski V.V. Some results for nonsymmetric dual-ring token-passing local area network. Modern mathematical methods of analysis and optimization of telecommunication networks: Queues: flows, systems, networks. BWWQT–2003. – Vol. 17., 2003. – P.58-60.