Bertiscanova Ê.Ò., Berdalieva À.À.
Karaganda State University named after E.A.Buketov,
Kazakhstan
About
interrelation of teaching materials of algebra and geometry at training of
concept of relation
Knowledge and abilities that pupils are getting during
the study of the course of mathematics, should not be the simple mechanical sum
of them. The solution of many mathematical problems is based on application of
system of knowledge not only by one discipline. The quality of pupils´
studying depends on application of various components of scientific knowledge by
algebra and geometry in their interrelation. Therefore, in the article is
considered the question of interrelation of teaching materials of algebra and
geometry while training the pupils to the school mathematics on example of
concept of the relation.
The set-theoretical approach is taken as a principal
in the school course of mathematics [1]. It allows us to enter some set-theoretical
concepts during some question studying. One of these general concepts of
mathematics is the concept of relation which is not defined and is given by
means of the description. The relation can be considered both between elements
of one set and between elements of two sets. Thus speaking about the relation
between sets we deal with set of ordered pairs, pairs that are in the given
relation. The relation between two sets can be defined with the set of points
of the plane with co-ordinates x and y, i.e. graphically. In other words, some
set of points of a co-ordinate plane is the graph of relation between abscissas
and ordinates of points.
The special kind of the relation is the concept of
mapping which can be considered as: maps of number sets on number sets (number
functions); maps of number sets on dot
sets (a method of co-ordinates); maps of sets of geometrical figures on number
sets (measurement of geometrical values); maps of dot sets on dot sets
(geometrical transformations) [2]. Such peculiarity of concept of mapping,
extending on many questions of a school course of mathematics, gives the chance
during some concepts studying to pass from
algebraic language on geometrical and vice versa. It allows to establish interrelation
in studying of algebraic and geometrical materials, to lead integration at
studying of related questions of mathematics [3].
The concept of function of a school course of
mathematics is entered on the basis of the general concept of the relation.
Such concepts as domain, range of reflection, graph of reflection, etc. are
entered into mathematics with concept of reflection.
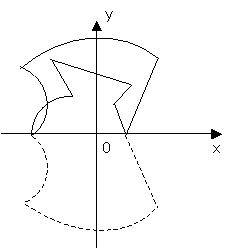
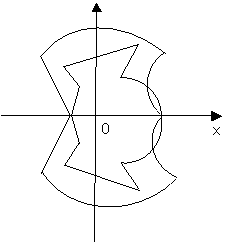
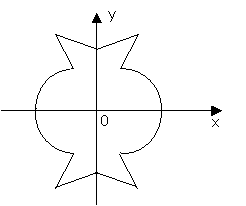
It is known, that function is the relation special
case, namely, any function is the relation, but not any relation can be a
function. Really, there are graphs of some sets of points of a co-ordinate
plane on two pictures (see pictures 1 and 2), in other words, the graphs of
relations between abscissas and ordinates of these points.
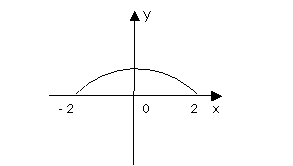



Ðic. 1 Ðic. 2
In the first case (pic. 1) we have the graph of
relation which is a function, in the second case (pic. 2) – there is some
relation which is not the graph of a function. If some relation between
elements of two sets is a function it means that to each element of one set
there corresponds a unique element of another set. Here the first set is the domain
of the given relation (in our case, of function), and the second is the range of
this relation. Thus, the concept of function is treated as correspondence and
the last concept is initial concept. Authors of modern school textbooks
consider the concept of function as some correspondence because in such
representation the concept of function becomes intuitively possible and
accessible to pupils.
There is no a distinction between concepts of relation
and correspondence in the school textbooks. The definition of function accepted
by authors of modern school textbooks, gives the chance to consider only
concept of relation because the general theory of relations and correspondences
does not play a special role in the course of mathematics for pupils [2]. The
relation between sets is defined by the law of correspondence which is
established by means of formula or by description.
The concept of function, as some subset of the relation
as its specific difference, is one of fundamental concepts of mathematics. For
the first time the term "function" has been entered into a science at
the end of 17 century and only in 1918 it began to be applied in a secondary
school course.
The concept of function has big theoretical and
practical value. In the school course of
mathematics acquaintance with concept of function, with the first graph of function
(linear) begins in 6 form and comes to the end in 11 form with studying of exponential, logarithmic and power functions. Therefore studying of a theme
"Function" represents one of the important methodical lines of a
school course of mathematics.
Studying the concept of function, pupils get
acquainted with variables, which are more than constants. It is known, that
there are not many constants in nature, and in mathematics. As an example of a
constant in mathematics, it is possible to talk about two formulas (the
relation of the circle´s length to its diameter and the sum of interior angles
in a triangle) which do not depend on the chosen values. One type of variables
changes arbitrary, and others - in certain dependence, last values represent a
subject of special studying in mathematics.
In the school course of mathematics the graph of
relation is not a subject of special studying. But this concept is the main
base for the course of mathematics in the 6-8 th forms. So, the concept of
relation and its graph can be considered more deeply in the high school to
generalize and systematize the pupils’ knowledge by the theme
"Function".
And now, let's
talk about the graph of relation. For this purpose let's examine various
variants of the same relation between the elements of sets. This is relation
with an absolute value. Besides, we will stop at the link between the given
algebraic problem and concept of symmetry from geometry course which is carried
out by the set-theoretical approach.
Pupils get acquainted with concept of symmetry in 6 form, and its regular studying begins in 9 form in part «Transformation of figures».This concept plays the
important role at studying geometry and has a wide application not only in
geometry, but also in reality. Ideally beautiful forms of buildings and other constructions, patterns
on fabrics, room wall-papers, leaves of plants, wings of butterfly and others often contains elements
of symmetry, more precisely, are
symmetric concerning some axis. Therefore it is necessary to pay an attention
for studying the theme «Axial symmetry».There are not enough time in the school
course of geometry to study the symmetry question. This question´s
studying has fragmentary character. So pupils have incomplete, superficial idea
about this theme. Meanwhile returning to idea of symmetry at lessons not only
in a geometry course, but also in algebra would allow to develop pupil´s space
imagination and to acquire properties of figures more strongly, for example, while
constructing the graphs of functions with an absolute value. It is possible to
connect closely the question about the relations´ graphs with axial
symmetry. Let´s consider how the symmetry concerning the axis can be represented
in analytical form, and vice versa. It becomes possible due to the property of
relation´s symmetry. Pupils should have representations about properties
of relations to consider this question. Such approach of teaching the properties
that carry out the connection between materials of courses of algebra and
geometry will allow to systematize pupils´ knowledge, to make them more realized
and strong.
There are the main types of the graph of the function
with an absolute value: ![]() ;
; ![]() ;
; ![]() . In the school course of
mathematics one of the simplest types of graph of the given functions is
. In the school course of
mathematics one of the simplest types of graph of the given functions is ![]() . From these main types by various combinations of the module sign it is
possible to receive the following types of relations:
. From these main types by various combinations of the module sign it is
possible to receive the following types of relations:
1. ![]() . 13.
. 13. ![]() .
.
2. ![]() . 14.
. 14. ![]() .
.
3. ![]() . 15.
. 15. ![]() .
.
4. ![]() . 16.
. 16. ![]() .
.
5. ![]() . 17.
. 17. ![]() .
.
6. ![]() . 18.
. 18. ![]() .
.
7. ![]() . 19.
. 19.![]() .
.
8. ![]() . 20.
. 20. ![]() .
.
9. ![]() . 21.
. 21. ![]() .
.
10.![]() . 22.
. 22. ![]() .
.
11. ![]() . 23.
. 23. ![]() .
.
12. ![]() .
.

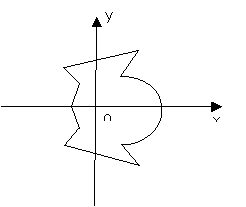
As it was said earlier, we will consider not, but some
set of points of co-ordinate plane (relation), represented on pic. 3 and we
will plot various graphs of the given relation.
Pic.3
While plotting the graphs we should use not only the
concept of symmetry but also the concept of an absolute value of a number that
is not resulted here.
We will consider the graphs of relations ![]() ,
, ![]() ,
, ![]() as elementary and won’t pay attention to their
plotting. We will note only that graphs
of relations
as elementary and won’t pay attention to their
plotting. We will note only that graphs
of relations ![]() and
and ![]() - are symmetric in y-axis and
graphs of relations
- are symmetric in y-axis and
graphs of relations ![]() and
and ![]() - are symmetric in x-axis.
- are symmetric in x-axis.
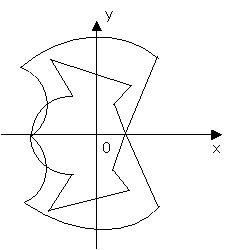
Let's consider more detail the plotting of some graphs
of relations from the offered system of tasks.
 1. The graph of relation
1. The graph of relation ![]() , is symmetric in the y-axis. Therefore at first we plot the part of
graph at non-negative values of õ, and then we will take the symmetry in the y-axis
(pic. 4). If to bend a sheet of paper on the y-axis the left and right parts of
the relation´s graph will coincide.
, is symmetric in the y-axis. Therefore at first we plot the part of
graph at non-negative values of õ, and then we will take the symmetry in the y-axis
(pic. 4). If to bend a sheet of paper on the y-axis the left and right parts of
the relation´s graph will coincide.
Pic.4 Pic.5
3. For plotting the graph of relation ![]() , proceeding from the definition of the absolute value of a real number
and symmetry of the graph in the y-axis, we will consider two graphs of
relations: a)
, proceeding from the definition of the absolute value of a real number
and symmetry of the graph in the y-axis, we will consider two graphs of
relations: a) ![]() , at x ≥ 0; and
, at x ≥ 0; and ![]() , at x < 0. The graph of the given relation is presented in at the
picture 5.
, at x < 0. The graph of the given relation is presented in at the
picture 5.
 4. We obtain the graph of relation
4. We obtain the graph of relation ![]() from the graph that is
represented at the picture 5, by taking the symmetry with respect to the x-axis
(pic. 6).
from the graph that is
represented at the picture 5, by taking the symmetry with respect to the x-axis
(pic. 6).
Pic.6 Pic.7
5. The graph of relation set by formula ![]() , will be situated in the top half plane, i.e. above the x-axis ,
including the axis itself because the expression
, will be situated in the top half plane, i.e. above the x-axis ,
including the axis itself because the expression ![]() is inside an absolute value.
Therefore we keep the part of the graph above the x-axis, and symmetrically
reflect in the x-axis the part of the graph which is below the x-axis (pic. 7).
is inside an absolute value.
Therefore we keep the part of the graph above the x-axis, and symmetrically
reflect in the x-axis the part of the graph which is below the x-axis (pic. 7).
 6. The graphs of relations
6. The graphs of relations ![]() and
and ![]() (pic.7) are symmetric in the y-axis. So we can easily plot the
graph of
(pic.7) are symmetric in the y-axis. So we can easily plot the
graph of ![]() (pic.8).
(pic.8).

Pic.8 Pic.9
7. We obtain
the graph of relation ![]() from the graph of relation
from the graph of relation ![]() (pic.7) by symmetric reflection in the x-axis (pic.9).
(pic.7) by symmetric reflection in the x-axis (pic.9).
 9. The graph of relation
9. The graph of relation ![]() is symmetric in y-axis, because the variable is inside of absolute
value and is situated above the x-axis, because the whole expression
is symmetric in y-axis, because the variable is inside of absolute
value and is situated above the x-axis, because the whole expression ![]() is inside of absolute value. The given graph is turned out from
the graph of relation
is inside of absolute value. The given graph is turned out from
the graph of relation ![]() (pic.4) by symmetric reflection in the x-axis. The graph received in this way is presented at picture 10.
(pic.4) by symmetric reflection in the x-axis. The graph received in this way is presented at picture 10.
Pic.10 Pic.11
11. As in the previous task (pic.10)
the graph ![]() is symmetric in the y-axis and will be
situated above the x-axis, including this axis. As the initial graph the graph
of relation
is symmetric in the y-axis and will be
situated above the x-axis, including this axis. As the initial graph the graph
of relation ![]() (pic. 5) is taken. The given graph
is presented at picture 11.
(pic. 5) is taken. The given graph
is presented at picture 11.
13. The relation set by the formula ![]() has a property of symmetry in
the x-axis. The given relation has the condition
has a property of symmetry in
the x-axis. The given relation has the condition ![]() , so let´s plot its graph,
keeping the top part that is above the x-axis without changing, and reflect it
symmetrically in the x-axis (pic.12). If to bend a
sheet of paper on the x-axis the top and bottom parts of the given relation’s graph
will coincide.
, so let´s plot its graph,
keeping the top part that is above the x-axis without changing, and reflect it
symmetrically in the x-axis (pic.12). If to bend a
sheet of paper on the x-axis the top and bottom parts of the given relation’s graph
will coincide.

Pic.12 Pic.13
15. The graph of relation ![]() can be easily obtained from the graph of relation
can be easily obtained from the graph of relation ![]() (pic.12), if we take the symmetry in the y-axis. By another way,
we plot the graph of relation
(pic.12), if we take the symmetry in the y-axis. By another way,
we plot the graph of relation ![]() , keep its top part and reflect
symmetrically in the x-axis (pic.13).
, keep its top part and reflect
symmetrically in the x-axis (pic.13).
17. To plot the graph of relation ![]() let´s use the graph of relation
let´s use the graph of relation ![]() (pic.7), and then take the symmetry of it with respect to the
x-axis (pic.14).
(pic.7), and then take the symmetry of it with respect to the
x-axis (pic.14).
Pic.14 Pic.15
18. To obtain the graph of relation ![]() we take the symmetry of the
graph of relation
we take the symmetry of the
graph of relation ![]() with respect to the y-axis. By another way, we can use the graph
of the relation y
with respect to the y-axis. By another way, we can use the graph
of the relation y ![]() (pic.8) and reflect it symmetrically in the x-axis (pic.15).
(pic.8) and reflect it symmetrically in the x-axis (pic.15).

 19. Let’s plot the graph of relation
19. Let’s plot the graph of relation ![]() . Here we have the doubled symmetry:
as in the x-axis and in y-axis as well. If
to bend a sheet of paper on the co-ordinate axes the parts of the given relation’s
graph will coincide (pic.16). The graph of the given relation can be also
obtained from the graph of relations that are drawn on the pictures 4 and 12.
In the first case we keep the top part of the graph
. Here we have the doubled symmetry:
as in the x-axis and in y-axis as well. If
to bend a sheet of paper on the co-ordinate axes the parts of the given relation’s
graph will coincide (pic.16). The graph of the given relation can be also
obtained from the graph of relations that are drawn on the pictures 4 and 12.
In the first case we keep the top part of the graph ![]() , that is above the x-axis and symmetrically
reflect it in the x-axis. In the second case we take the symmetry twice of the
part of the relation’s graph
, that is above the x-axis and symmetrically
reflect it in the x-axis. In the second case we take the symmetry twice of the
part of the relation’s graph ![]() that is situated in the first quadrant with respect to the both
axes (pic.16).
that is situated in the first quadrant with respect to the both
axes (pic.16).
Pic.16
Pic.17
20. To plot
the graph of relation ![]() we can use the graphs of
relations:
we can use the graphs of
relations: ![]() (pic.5), we keep the part of the
graph that is in the first quadrant and take the symmetry twice with respect to
the co-ordinates axes; or we can use the graph
(pic.5), we keep the part of the
graph that is in the first quadrant and take the symmetry twice with respect to
the co-ordinates axes; or we can use the graph ![]() (pic.13), here we keep without
change the part of these graph at x ≥ 0 and reflect this part
symmetrically in the y-axis. In the both cases we obtain the graph of relation
represented at the picture 17.
(pic.13), here we keep without
change the part of these graph at x ≥ 0 and reflect this part
symmetrically in the y-axis. In the both cases we obtain the graph of relation
represented at the picture 17.
22. In this task ![]() we deal with three absolute
values and doubled symmetry: with respect to the both axes of co-ordinates. We
can use the graph of relation that is at the picture 10, by reflecting it
symmetrically in the x-axis (pic.18). Or we can use the graph of relation
we deal with three absolute
values and doubled symmetry: with respect to the both axes of co-ordinates. We
can use the graph of relation that is at the picture 10, by reflecting it
symmetrically in the x-axis (pic.18). Or we can use the graph of relation ![]() (pic.7) at x ≥ 0 and take
the symmetry twice with respect to the axes of co-ordinates. Also we can use
the graph of relation
(pic.7) at x ≥ 0 and take
the symmetry twice with respect to the axes of co-ordinates. Also we can use
the graph of relation ![]() (pic.14) at x ≥ 0 and
symmetrically reflect it in the y-axis.
(pic.14) at x ≥ 0 and
symmetrically reflect it in the y-axis.

Pic.18 Pic.19
23. To construct the graph of relation ![]() let´s use the graph of
relation
let´s use the graph of
relation ![]() (pic.5). At first we take the
symmetry of the bottom part of the graph with respect to the x-axis, keeping
the part of the graph that is in the first quadrant we take the symmetry two
times in the axes of co-ordinates (pic.19). Or we can obtain the given graph
from the graph of relation
(pic.5). At first we take the
symmetry of the bottom part of the graph with respect to the x-axis, keeping
the part of the graph that is in the first quadrant we take the symmetry two
times in the axes of co-ordinates (pic.19). Or we can obtain the given graph
from the graph of relation ![]() (pic.11) by reflecting it
symmetrically in the x-axis.
(pic.11) by reflecting it
symmetrically in the x-axis.
The rest numbers: 2, 8, 10, 12, 14, 16, 21 we suggest
to do by yourselves.
Carrying out this system of tasks above, pupils study
to analyze, abstract the particular objects, situations. Designing various
images, they develop the space imagination; start to learn the mathematical
objects in movement, and also the connections between algebra and geometry.
Besides, the research skills are formulated because such tasks have no certain
stereotype of solution.
Teachers can use the materials of this article, system
of the developed tasks as additional lessons by mathematics, at planning and
performance of scientific projects, and also at lessons of the elementary
mathematics for students.