Карачун В.В., Мельник В.Н., Кладун Е.А., Ковалець О.Я.

Национальный технический университет Украины «КПИ»

УПРУГО-ДЕФОРМИРОВАННОЕ СОСТОЯНИЕ КРЫШКИ КОЖУХА ГИРОИНТЕГРАТОРА В АКУСТИЧЕСКИХ ПОЛЯХ. НЕСТАЦИОНАРНАЯ ЗАДАЧА

В случае нестационарного упругого взаимодействия, дифференциальное уравнение возмущенного изгибного движения торцевой пластины кожуха имеет вид:

, (1)

где ; - время; - прогиб крышки; , - соответственно, цилиндрическая жесткость, плотность материала, толщина и коэффициент Пуассона.

Правую часть этого уравнения зададим следующим образом –

, (2)

где , а ограничения на величину этого параметра уточним далее.

Решение уравнения (1) ищем в виде

. (3)

Множитель , который не зависит от времени , назовем амплитудой изгибных колебаний.

Подставляя (3) в исходное уравнение (1), получаем

, (4)

где .

Найдем приближенные решения в форме

. (5)

Столбец

(6)

подлежит определению.

Подстановка (5) в (4) приводит к приближенному равенству

, (7)

для которого столбец (6) считаем наиболее подходящим в том смысле, чтобы проекции левой и правой частей выражения (7) на линейную оболочку образов координатных функций были бы равны.

Умножив обе части равенства (7) на

,

получаем:

. (8)

Матрица Грама образов координатных функций

найдена ранее и описана формулой:

.

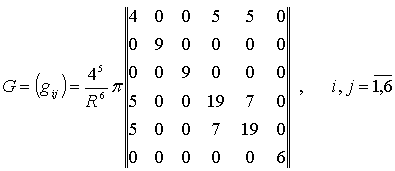Столбец также найден и представлен соотношением:

.

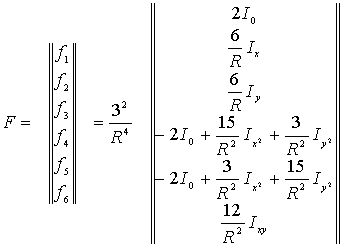Таким образом, остается составить матрицу

, (9)

которую назовем матрицей Грама координатных функций по энергии оператора . После вычислений получаем –

. (10)

Зная матрицу Грама образов координатных функций и матрицу Грама координатных функций по энергии оператора (10), систему (8) можно записать иначе –

. (11)

Если , то эта система однозначно разрешима, то есть

, (12)

и можно строить приближенное решение уравнения (4) в форме (5).

Так как матрица неособенная (невырожденная), то

,

где - единичная матрица. Тогда

;

.

Но есть многочлен степени относительно . Если является положительным корнем этого уравнения, то система (11) может оказаться неразрешимой.

Проанализируем этот факт подробнее. Положим для простоты уравнение однородным –

, (13)

где , при однородных граничных условиях.

Ненулевые решения ищем в виде –

, (14)

где множитель удовлетворяет граничным условиям.

Подставляя (14) в уравнение (13), получаем:

;

, (15)

где . Тогда

. (16)

Приближенное решение задачи (15) отыскиваем в виде –

(17)

где - координатные функции.

После подстановки выражения (17) в соотношение (15), получаем приближенное равенство

(18)

с неизвестным столбцом .

Как и ранее, наилучшим считаем столбец, при котором проекции левой и правой частей выражения (18) на линейную оболочку образов координатных функций равны друг другу, то есть

.

Столбец не должен быть нулевым, поэтому

.

Из положительной определенности оператора вытекает, что , а, значит, есть положительные корни многочлена . В нашей задаче они представляются приближенными собственными числами оператора .

Принимая во внимание, что , из выражения (16) находим:

.

Это значит, что в принятом приближении собственные частоты определяются соотношениями –

.

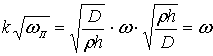Следовательно, чтобы задача (4) нахождения вынужденных колебаний торцов была разрешимой, необходимо исключить совпадение частот плотности возмущающего акустического воздействия и собственной. Другими словами – избежать частотного резонанса.

Если ограничиться только первыми тремя координатными функциями

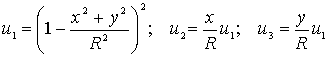
и их образами

; ; ,

то матрица окажется диагональной –

. (19)

Нули ее определителя будут наблюдаться при условии, когда

;

с одновременным выполнением соотношения

.

Для принятых числовых значений, когда , значения этих частот будут такими –

; .

Резонансными частотами являются:

; ,

где .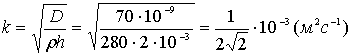

Численный анализ величины дает возможность определить резонансные частоты (рис.1). Они составляют , , и .

Количественную оценку прогибов торца проведем в диапазоне частот с шагом 1000, для , , .

Величина прогиба есть комплексное число

,

где , , а функции задаются; ; - определяется матрицей (19); ; ; ; ; ; (); , шаг 0,001.

Естественно, что с течением времени фаза колебаний меняет знак. Так, в момент времени , что составляет около секунды, амплитуда прогиба в центре торца составляла , при - , а при прогиб равен нулю и пластина занимает исходное свое положение – кривые 1, 2 и 6 соответственно.

Далее, с увеличением , фаза прогиба меняет знак и изгибное движение пластины начинает происходить в противоположном. Таким образом, через определенное время происходят своеобразные «хлопки» торцевой пластины.

Вообще говоря, торцы кожуха гироскопа находятся не в одинаковых условиях с точки зрения акустического нагружения. Дифракция звуковой волны внутри подвеса может менять структуру поля совершенно случайным образом. Поэтому не будет наблюдаться полная симметрия в пространстве и во времени акустической вибрации.