Бондаренко Л. Н., Матвиец Т. В., Бондаренко В. Д., Матвиец И. В.

Приднепровская государственная академия строительства и архитектуры

Аналитическое определение составляющих сопротивления

качению шара от скольжения

Введение. При расчете сопротивления движению шара по основанию любой конфигурации используется коэффициент трения качения, как производная от полуширины пятна контакта [1-3]. Конечно, такое решение определяет только «чистое» качение. Но при качении возникают и сопротивления от проскальзывания шара в месте контакта. Это сопротивление возникает только при контакте тел с разными величинами упругости. Считается также, что микропроскальзывание возникает также и вследствие разной кривизны двух тел.

Но в месте контакта кривизны обоих контактируемых тел одинаковы, поэтому последнее утверждение необходимо поставить под сомнение. Дело в том, что радиус качения, например шара по плоскости, является переменным на длине пятна контакта и микроскольжения будут возникать из-за этого. Поэтому необходимо установить, какую долю сопротивления качению занимает эта составляющая от общего.

Проблема микропроскальзываний на контакте двух тел при качении качественно рассматривалась Рейнольдсом [4], а количественно она рассмотрена почти через сто лет Табором [3] экспериментально.

Табором же получены аналитические зависимости для определения коэффициента трения качения, но наличие в них коэффициента гистерезисных потерь не позволяет использовать их в инженерной практике. Естественно, в этом случае невозможно выделить из экспериментальной величины сопротивления качению составляющую, припадающую на чистое качение.

Постановка задачи и ее решение.

Вследствие разной величины радиуса качения шара возникают микропроскальзывания, но неизвестно, какую часть они составляют от общего сопротивления, поэтому, в дальнейшем установим приведенный коэффициент трения качения от микропроскальзываний в месте контакта шара вследствие разного радиуса качения по длине пятна контакта.

Рассмотрим сначала схему касания шар-плоскость (рис.1).

Рис.1. Расчетная схема для касания сферическое тело-площадь

Сближение контактирующих тел находится из теории контактных деформаций Герца [4]. Будем считать, что максимальная деформация шара в точке О составляет половину от . Это допущение может быть проверенно так. Длина хорды АВ равняется 2а и высота сегмента составляет , а сумма должна составлять радиус шара. В дальнейшем будет доказано, что полученная величина радиуса будет отличаться от действительной меньше, чем на 1%. Таким образом, сближение тел при контакте осуществляется за счет местных деформаций. Исходя из этого

, (1)

Радиус шара определим исходя из теории контактных напряжений Герца

, (2)

Расстояние от центра шара до точки О

. (3)

Поскольку полуширина пятна контакта

, (4)

то расстояние из рис. 1

. (5)

Если допустить, что радиус шара меняется от точки О до точки А по треугольнику, то средняя скорость проскальзывания

, (6)

где

, . (7)

При нагрузке на шар Р и коэффициенте трения скольжения мощность на скольжение

. (8)

Мощность, необходимая на преодоление общего сопротивления качению шара, включающая и чистое качение

, (9)

где - коэффициент трения качения.

В [6] доказано, что величина при начальном точечном контакте находится из выражения

. (10)

Приравняв выражения (8) и (9) можно найти приведенный коэффициент трения качения от проскальзывания

. 11)

Формула (10) получена экспериментально - аналитически. Поскольку эксперименты проводились для крановых колес при (сталь по стали без смазки), то для определения коэффициента трения качения от чистого качения необходимо из общей величины (10) вычесть величину, приходящуюся на скольжение (11) при и эта величина будет постоянной при любом

. (12)

Расчеты, проведенные по полученным формулам показывают, что, например, при Р=25 кН и МПа мм; мм, а составляющая, приходящаяся на скольжение при качении шара по плоскости, равна от тысячных долей процента при (смазка жидкостная в масляной ванне) до 0, 02% при .

Рассмотрим эту же задачу для схемы касания сферическое тело – круговой желоб (рис. 2). Местная деформация шара при условии, что радиус желоба

, (13)

где - коэффициент, зависящий от соотношения коэффициентов уравнения эллипса касания.

Радиус шара найдется из выражения

. (14)

Половина длины пятна контакта

, (15)

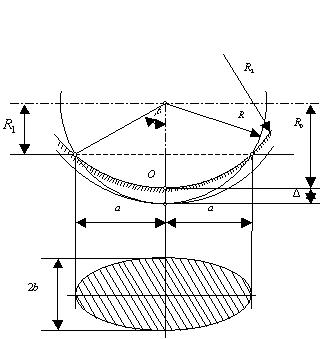
Рис. 2. Расчетная схема для касания сферическое тело – желоб

Полуширина пятна контакта найдется из выражения (15) при замене на .

В дальнейших расчетах необходимо воспользоваться формулами (5) – (15).

Расчеты, проведенные для этой схемы контакта при принятых в предыдущем примере величинах Р и Е показывают, что доля припадающая на скольжение, как и следовало ожидать, в несколько раз больше, чем в предыдущем примере, но даже при не превышает нескольких десятых процента.

Выводы.

1. Доля сопротивлению качению шара, приходящаяся на скольжение в месте контакта, не превышает нескольких десятых процента от общего (для металлов);

2. Полученные аналитически результаты подтверждаются экспериментальными исследованиями Табора [3].

Литература

1. Довбня Н.П., Бондаренко Л.Н., Бобырь Д.В. и др. Соотношение между сопротивлением качению и скольжению в роликовых подшипниках букс / Проблемы трибологии. – Хмельницкий: ТУП.-2007.-№4.-с. 36-38.

2. Джонсон К. Механика контактного взаимодействия.– М.: Мир, 1989. - 510 с.

3. Tabor D. The mechanism of rolling friction; the elastic range. – Proc. Roy. Soc., 1955. - P. 198.

4. Reynolgs O. On rolling frictionh. – Philos. Trans. Roy.Soc., 1875.-P.155

5. Справочник по сопротивлению материалов / Писаренко Г.С., Яковлев А.П., Матвеев В.В. – К.: Наук. думка, 1988. - 736 с.

6. Бондаренко Л.Н., Довбня Н.П., Поветкин В.С. Деформационные сопротивления в машинах. – Днепропетровск: Дніпро – VAL. – 202.-200 с.