Матвієць Т.В., Бондаренко В.Д., Бондаренко Л.М., Маслюк В. С.

Придніпровська державна академія будівництва та архітектури

Вплив опору коченню на точність рішення задач з коченням

Вступ. В задачах з коченням коефіцієнт тертя кочення, наприклад в [1], для пари колесо-рейка рекомендується приймати рівним 0,05 мм, а в [2] його значення прийняті залежними від діаметра колеса і величина коливається від при діаметрі колеса мм до при мм (для плоскої головки рейки). Такі значні розходження у величинах коефіцієнта тертя кочення не можуть не впливати на кінцеві результати при рішенні задач з коченням.

Отримана в [2] експериментальна залежність між діаметром колеса і коефіцієнтом тертя кочення наводить на думку про залежність від ширини плями контакту в напрямку руху колеса.

Така залежність отримана Табором [3], яка при початковому лінійному контакті має вигляд:

, (1)

де - півширина плями контакту; - коефіцієнт гістерезисних витрат.

Автор цієї формули стверджує, що величина мала, очевидно мається на увазі, що вона не значно відрізняється від одиниці.

Наявність в формулі (1) коефіцієнта зводить на нівець її практичне використання, оскільки не існує методики його визначення.

В [4] отримана експериментально-аналітична залежність, яка для початкового лінійного контакту має вигляд:

, (2)

де - радіус колеса в метрах.

Порівняння формул (1) і (2) показує, що коефіцієнт гістерезисних витрат .

В подальшому встановимо частку складової на опір коченню від гістерезисних витрат, а також знайдемо мінімальну силу при якій починається рух колеса при силі тиску на колесо, знайденій із величини допустимих контактних напружень.

Скориставшись формулою (2) отримаємо кінцеві результати рішення задачі наведеної в [1]. В декілька скороченому вигляді задача формулюється так.

Котушка (дальше – циліндричне колесо) вагою і радіусом приводиться в рух через нитку , яка змотується з неї; нитка розташована під кутом до горизонту. До нитки прикладена постійна сила . Необхідно визначити швидкість центру мас С колеса в момент, коли воно переміститься на відстань s. Котушка котиться без ковзання. Масою нитки знехтувати. Радіус кільця, на яке намотується нитка . У початковий момент система знаходиться в спокої.

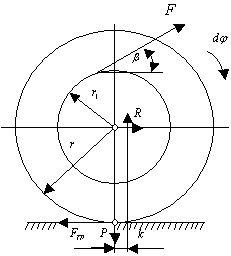
Рис. 1. Схема до умови задачі.

Не повторюючи повністю рішення задачі, запишемо вираз для роботи зовнішніх сил на переміщені s

. (3)

Кінетична енергія в кінцевому положенні (у припущені, що радіус інерції котушки малий)

Швидкість центру мас котушки:

; (4)

визначимо. що в [1] в цій формулі допущена описка.

Спочатку знайдемо радіус у залежності від величини приведеної ваги колеса P, прийнявши вагу рівній 30; 50; 70; 90 кН.

Скориставшись теорією контактних напружень Герца [5] та прийнявши коефіцієнт Пуассона матеріалів колеса та площини рівними 0,3, отримаємо

, (5)

де B - ширина рейки; - допустимі контактні напруження; E - модуль пружності матеріалів колеса та рейки.

Півширина плями контакту

Залежності коефіцієнта тертя кочення від P при B = 40 мм; МПа; і МПа показані на рис. 2.

Рис.2. Залежності від приведеної ваги колеса коефіцієнта тертя кочення: 1 - ; 2 - МПа; 3 – по [1]; 4 – по [2]; - без врахування коефіцієнта гістерезисних витрат.

Залежності швидкості центру мас колеса від шляху переміщення при Р = 30 кН, і МПа показані на рис.3.

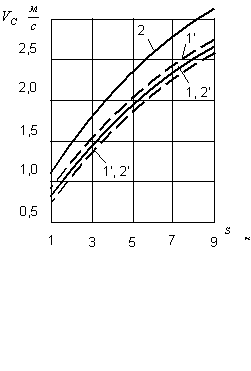
Рис. 3. Залежності швидкості центру мас колеса від шляху переміщення при Р = 30 кН, (1) і МПа (2); - без врахування коефіцієнта гістерезисних витрат; - по [1].

Залежності мінімальної сили F при якій починається рух колеса від P показані на рис. 4

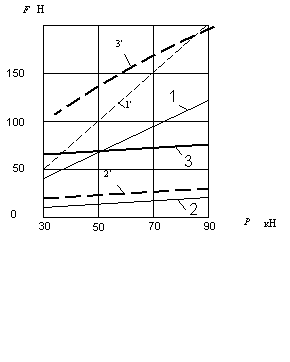
Рис. 4. Залежності мінімальної сили, прикладеної до нитки, при якій починається кочення колеса від приведеної ваги колеса: 1 - ; 1' - МПа; 2 – теж по [1] при МПа; 2' - теж по [2] при МПа; 3 – по [2] при МПа; 3' – теж при МПа.

Аналіз графіків на рис.2, рис.3, рис. 4, дозволяють зробити такі висновки:

- частка складової від гістерезисних витрат в коефіцієнті тертя кочення залежить від радіуса колеса, збільшуючись з його збільшенням і досягає біля 50% при Р = 90 кН і МПа;

- швидкість центру мас колеса значно залежить від допустимих контактних напружень, збільшуючись з їх збільшенням;

- мінімальна сила, при якій починається рух колеса при силі, знайденій із величини допустимих контактних напружень, збільшується зі збільшенням допустимих напружень.

Література:

1. Тарг С.М. Краткий курс теоретической механики.-М.: Наука, 1970.-478 с.

2. Справочник по кранам: В 2 т. Т.2/ Александров М.П., Гохберг М.М., Ковин А.А. и др. – Л.: Машиностроение, 1988.-559 с.

3. Tabor D. The mechanism of rolling friction: the elastic rande. – Proc.Roy.Soc., 1955.-P.198.

4. Бондаренко Л.М. Аналітично-експерементальне визначення коефіцієнта тертя кочення / Будівництво України.-2001.-С. 47-48.

5. Справочник по сопротивлению материалов / Писаренко Г.С., Яковлев В.В. – Киев: Наук.думка, 1988.-736с.