Современные информационные технологии /4.Информационная безопасность.

Галушко С. А., Милинчук Ю. А., Жукова Е.А.

Государственное высшее учебное заведение «Национальный горный университет»

Применение критерия c² Пирсона для проверки гипотезы о законе распределения случайных и псевдослучайных последовательностей

При построении ключевых систем шифрования одной из основных задач является получение случайных и псевдослучайных последовательностей, которые неотличимы от случайных и обладают большим периодом. После генерации последовательности чисел X = {x₁, x₂, …, x_n} необходимо убедиться, что случайная величина Х обладает равномерным законом распределения, её реализации случайны и независимы. Математическая статистика дает нам возможность построить статистические тесты для проверки гипотез о равномерности, случайности и независимости случайных величин.

Для проверки гипотезы о законе распределения воспользуемся критерием c² Пирсона.

Рассмотрим сущность этого критерия.

Критерий Пирсона или критерий χ²— наиболее часто употребляемый критерий для проверки гипотезы о законе распределения. Во многих практических задачах точный закон распределения неизвестен, то есть является гипотезой, которая требует статистической проверки. Обозначим через X исследуемую случайную величину. Пусть требуется проверить гипотезу H₀ о том, что эта случайная величина подчиняется закону распределения F(x). Для проверки гипотезы произведём выборку, состоящую из n независимых наблюдений над случайной величиной X. По выборке можно построить эмпирическое распределение F ^* (x) исследуемой случайной величины. Сравнение эмпирического F ^* (x) и теоретического распределений производится с помощью специально подобранной случайной величины — критерия согласия. Одним из таких критериев и является критерий Пирсона.

В наиболее часто используемом на практике критерии Пирсона в качестве меры расхождения U берется величина («хи - квадрат»):

(2)

где – эмпирические (опытные) частоты случайной величины X; – теоретические частоты, представляющие произведение числа наблюдений n на вероятности , рассчитанные по предполагаемому теоретическому распределению.

Доказано, что выборочная характеристика или, как ее еще называют, статистика при имеет – распределение с степенями свободы, где т – число интервалов эмпирического распределения (вариационного ряда); r – число параметров теоретического распределения, определяемых по опытным данным (например, в случае нормального закона распределения число оцениваемых по выборке параметров ). Схема применения критерия сводится к следующему:

1. Определяется мера расхождения эмпирических и теоретических частот по формуле (2).

2. Для выбранного уровня значимости по таблице – распределения находят критическое значение  при числе степеней свободы .

3. Если фактически наблюдаемое значение больше критического, то есть гипотеза отвергается, если , то гипотеза не противоречит опытным данным.

Замечание 1. Если в таблице – распределения приводятся вероятности , то гипотеза отвергается, если вероятность меньше выбранного уровня значимости, то есть и принимается в противном случае.

Замечание 2. Критерии Пирсона дает удовлетворительные результаты, если в каждом группировочном интервале достаточное число наблюдений ; если в каком-нибудь интервале число наблюдений меньше 5, имеет смысл объединить соседние интервалы с тем, чтобы в объединенных интервалах, было не меньше 5. При вычислении числа степеней свободы k в качестве т берется соответственно уменьшенное число интервалов.

Таким образом, оценка закона распределения по данным выборки (например, по выборочному распределению) предполагает последовательное решение трех проблем:

1) выбор типа теоретического (генерального) распределения и определение его параметров по результатам выборки;

2) построение теоретического ряда по найденному закону распределения или решение отдельных частных задач;

3) оценка расхождения (согласия) между теоретическим и опытным рядами.

Методика анализа результатов полученных на основе применения критерия Пирсона

Предлагается следующая методика использования критерия.

На основе критерия Пирсона строятся следующие тесты.

Тест 1. Проверяется расположение одномерных точек x₁, x₂, …, x_n в интервале 0 £ x £ 1, n – объем выборки. Интервал разбит на 16 подинтервалов. Вычисляется статистика

,

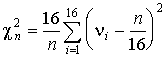где v_i – количество точек, попавших в интервал (i – 1)/16 £ x £ i/16. Значения c² вычисляются для выборок с объемами n = 600´2^s, где s = 0, 1,… ,17. В качестве показателя Ф₁, характеризующего прохождение данного теста выбирается значение c² по правилу

Ф₁ = , n = 600´2^s, s = 0, 1,… ,17.

Тест 2. Проверялось расположение двухмерных точек (x₁, x₂), (x₃, x₄), …, (x_2n-1, x_2n) в квадрате 0 < x, y< 1. Квадрат разбивался на 8² = 64 равных квадратов, и вычислялось значение

,

где n_ij – количество точек попавших в квадрат (i – 1)/8 £ x £ i/8; (j –1) £ u £ j/8, а n = 300´2^s, s = 0,1,…,17. В качестве показателя Ф₂, характеризующего прохождение данного теста выбирается значение c² по правилу

Ф₂ = , n = 300´2^s, s = 0,1,… ,17.

Тест 3. Проверялось расположение трехмерных точек (x₁, x₂, x₃), (x₄, x₅, x₆), …, (x_3n-2, x_3n-1, x_3n) в кубе 0 < x, y, z < 1. Куб разбивался на 5³ = 125 равных кубов и вычислялось значение

,

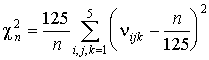где n_ijk – количество точек попавших в куб (i – 1)/5 £ x £ i/5; (j –1)/5 £ y £ j/5; (k –1)/5 £ z £ k/5, а n = 200´2^s, s = 0,1,…,17. В качестве показателя Ф₃, характеризующего прохождение данного теста выбирается значение c² по правилу

Ф₃ = , n = 200´2^s, s = 0,1,…,17.

Тест 4. Проверялось расположение четырехмерных точек (x₁, x₂, x₃, x₄), (x₅, x₆, x₇, x₈), …, (x_4n3, x_4n2, x_4n-1, x_4n) в гиперкубе 0 < x, y, z, q < 1. Гиперкуб разбивался на 4⁴ = 256 равных гиперкубов и вычислялось значение

,

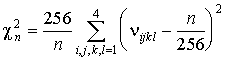где n_ijkl – количество точек попавших в гиперкуб (i – 1)/4 £ x £ i/4; (j –1)/4 £ y£ j/4; (k –1)/4 £ z £ k/4; (l –1)/4 £ q£ l/4, а n = 150´2^s, s = 0,1,…,17. В качестве показателя Ф₄, характеризующего прохождение данного теста выбирается значение c² по правилу

Ф₄ = , n = 150´2^s, s = 0,1,…,17.

Таким образом, формируется векторный показатель, характеризующий прохождение всех четырех тестов

.

В таблице 1 представлены пороговые значения c²_a для каждого из вышерассмотренных тестов. Здесь t – мерность теста (т.е. проверка одно-, двух-, трех-, и четырехмерных точек), a – доверительный уровень. Для выноса суждения о подтверждения гипотезы о равномерности закона распределения необходимо, чтобы величины Ф₁, Ф₂, Ф₃, Ф₄ были меньше, чем соответствующие пороговые значения c²_a.

Таблица 1.

a	t
	1	2	3	4
0.01	32	93,217	164,69	311,56
0.05	26,296	83,675	152,09	294,32
0.1	23,542	78,86	145.64	285,39

Опираясь на значения c²_n, полученные в каждом тесте, рассчитываются значения вероятности

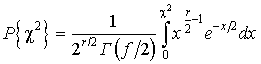
где r – степени свободы и строится график зависимости P{c²} = f(s) для каждого из тестов. Графики подвергаются анализу, в ходе которого определяются тенденции изменения значений вероятностей в зависимости от изменения объема выборок.

Однако, следует заметить, что однократное попадание величины c² в доверительный интервал ещё не означает уверенности в истинности гипотезы, равно как и однократный вылет c² за пределы интервала ещё не означает уверенности в ее ложности. В рассмотренных выше тестах решение принимается именно по однократному вычислению c².

Для повышения уверенности в суждении и получения дополнительной информации для принятия решения об обеспечении равномерности распределения псевдослучайных чисел проводятся следующие расчеты. В каждом из тестов, для каждой выборки рассчитывается 100 (или более 100) значений c². Естественно, каждый раз задается новое, отличное от других начальное состояние x₀ генератора. Затем определяется количество (в процентах) L_t,n значений c²_n попавших в доверительный интервал. При этом необходимо учитывать следующие особенности:

- естественно предположить, что при выборе определенного значения a количество значений c², удовлетворяющих критерию для данного a, должно составить не менее (1-a)*100 % от общего количества проведенных испытаний. На самом деле этот процент будет несколько ниже;

- если при многократном испытании с использованием критерия Пирсона величина c² не превысит порогового значения, но каждый раз будет мало отличаться от него, то это свидетельствует о необходимости проведения дополнительных исследований в виду недостаточного согласия гипотетического и эмпирического распределений.

Полученные значения L_t,n подвергаются анализу, в ходе которого нужно обратить внимание на корреляцию значений c²_n и L_k,n.

Окончательное решение принимается с учетом всей полученной информации.

и вычисляется по формуле

,

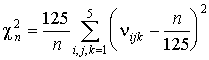где n_ijk – количество точек попавших в куб (i – 1)/5 £ x £ i/5; (j –1)/5 £ y £ j/5; (k –1)/5 £ z £ k/5, а n = 200´2^s, s = 0,1,…,17. В качестве показателя Ф₃, характеризующего прохождение данного теста выбирается значение c² по правилу

Ф₃ = , n = 200´2^s, s = 0,1,…,17.