Дифференциальные и интегральные уравне­ния

 

Ахажанов Т.Б.

Евразийский национальный университет им. Л.Н. Гумилева, г. Астана

ПРЯМЫЕ ТЕОРЕМЫ ТЕОРИИ ПРИБЛИЖЕНИЙ ФУНКЦИЙ ДВУХ ПЕРЕМЕННЫХ С ОГРАНИЧЕННОЙ P-ВАРИАЦИЕЙ ПОЛИНОМАМИ ХААРА ИЛИ УОЛША

 

В данной работе доказывается прямая теорема приближения функций двух переменных ограниченной p- вариации полиномами Хаара и Уолша.

Определения.  Пусть функция  определена на квадрате  и , где , - произвольное разбиение квадрата . Вариационной суммой порядка   функции  по разбиению назовем величину

Для функции одной переменной понятие вариационной суммы впервые ввел Винер [1], для функций двух переменных -Л.Кларксон и С.Адамс [2].

Вариационным модулем непрерывности    порядка   функции  называется величина

где , . Будем говорить, что , , если , и что , , если .  Свойства вариационного модуля непрерывности для функции одной переменной исследованы А.П. Терехиным [3], С.С. Волосивецем [4].  

Пространства   и  являются банаховыми с нормой

.

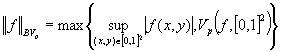Пусть теперь равна 1 на  и -1 на . Продолжим ее периодически с периодом 1 на всю ось. Тогда функциями Радамахера  называются функции ,.

Функции Уолша в нумерации Пэли определяются следующим образом (см. [5]). Положим . При  рассмотрим двоичную запись :

; ;  или , .

Тогда

n-я функция Уолша.

Функции системы Хаара на  задаются так:  при ; если же , ,  и ,

то

  .

Через

, ,

обозначим двумерные функции Хаара и Уолша. 

         Через ,  соответственно будем обозначать наилучше приближени функции  полиномами по системе Хаара (Уолша) порядка не выше  () в метрике , где ,  или ,

.

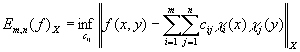Через ,  обозначим частичную сумму ряда Фурье по системе Хаара (Уолша) функции . Через  - обозначим положительные постоянные, зависящие от параметров , вообще говоря, различные в разных формулах.

         Основной целью данной работы является доказательство следующей теоремы, являющейся аналогом прямой теоремы теории приближения функций полиномами по системе Уолша или Хаара. Для доказательства теоремы нам понадобятся некоторые вспомогательные утверждения.

Лемма 1. Пусть ,, - такое разбиение квадрата  при ,.Тогда

.

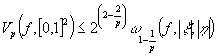Лемма 2. Пусть ,,  и ,  .Тогда верно неравенство

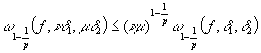
Доказательство. Пусть   разбиение квадрата такое, что , . Мы возьмем  новое подразбиение квадрата  

, , ,

содержащее точки  и разбивающее отрезки  ,  на  и  на равных частей соответственно. Тогда, на основании неравенства Гёльдера, имеем

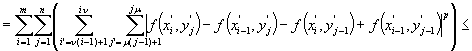
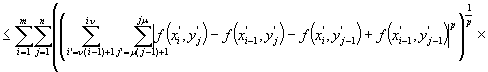
Отсюда взяв супремум, получим требуемое неравенство. Лемма 1 доказана.

Лемма 3.  Для частных сумм ,  ряда Фурье –Хаара или Уолша функций  имеет место формула

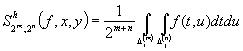 при    

или                                                                                                                                     

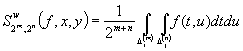 при .

Для функций одной переменной указанные равенства имеются в [5] стр. 45. Для случая функций двух переменных оно доказывается аналогично.

Лемма 4.  Любая функция  , постоянная на каждом прямоугольнике  , , , представима в виде полинома порядка не выше   по системе Хаара или Уолша.

В случае функций одной переменной такое равенство имеется в [5] стр. 22-23, 203-204.

Следствие 1. Для любого  имеет место равенство

.

Для случае функции одной переменной такое равенство имеет в [5] стр. 206. Для случая функций двух переменных оно доказывается аналогично.

         Теорема 1. Пусть ,,  .Тогда верны неравенства

 (1)

 (2)

Доказательство.  Чтобы получить (1) и (2), рассмотрим разбиение , где ,  и ступенчатую функцию , равную  на квадрате ,, . Согласно лемме 4,  является полиномом по системе Хаара (или Уолша) порядка не выше . Так, как , , то по лемме 1

.

 

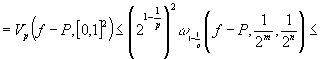
Поскольку  постоянна на множестве длины ,

 

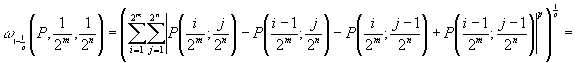
         Таким образом,

.

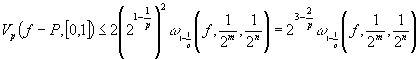Поэтому

,

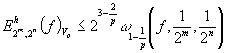если учесть неравенство

, .

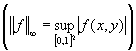При ,  воспользуемся тем, что ,  и леммой 2.

Имеем

 

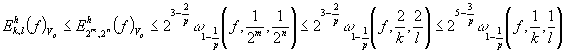
Неравенство (1) доказано. Пользуясь следствием 1 и последними выкладками, убеждаемся, что (2) также верно.

 

Литература

1.     N.Wiener. The quadratic variation of a function and its Fourier coefficients / Massachusetts J.Math., 3(1924), 72-94 с.

2.     J.A. Clarkson and C.R. Adams. On definitions of bounded variation for functions of two variables /  Trans. Amer. Math. Soc., 35(1933), 824-854 с.

3.     Терехин А.П. Приближение функций ограниченной p- вариации / Изв. Вузов. Математика. 1965. №2. 171-187 с.

4.     Волосивец С.С. Приближение функций ограниченной p- вариации полиномами по системам Хаара и Уолша / Мат. Заметки. 1993. Т 53. №6.  11-21 с.

5.     Б.И.Голубов, А.В.Ефимов, В.А.Скворцов. Ряды и преобразования Уолша: теория и применения. /  Москва «Наука», 1987 г.