Педагогические науки/5.Современные методы преподавания.

Галушко С.О., Мілінчук Ю.А, Жукова О.А.

Державний вищій навчальний заклад «Національний гірничій університет»

Розв’язання систем диференційних рівнянь.

В сучасний період розвитку обчислювальної техніки актуальність числових методів, що дозволяють розв’язувати широкий клас задач за допомогою ЕОМ, продовжує зростати. Розробник повинен вміти відокремлювати у загальній проблемі типові задачі та визначити методи, за допомогою яких їх можна розв’язати,також він повинен інтегрувати розв’язок задачі до специфічних потреб промисловості.

Завдання запропонуванні у наданій лабораторній роботі полягає у тому, щоб надати студентам досвід застосування числових методів до типових практичних задач прикладної математики із застосуванням ЕОМ. В якості інструментарію виконання робіт студентам пропонується застосувати середовище MathCAD.

Багато задач математики і фізики можна описати диференційними рівняннями виду y^’(x) = f(x,y). MathCAD має розвинуті засоби для чисельного рішення систем диференційних рівнянь.

Для рішення задач такого класу в MathCAD є ряд функцій. Розглянемо функції, які дають рішення для систем звичайних диференційних рівнянь:

_{Rkadapt (y, x1, x2, n, F) – повертає матрицю рішень методом Рунге-Кутта с змінним кроком для систем звичайних диференційних рівнянь з початковими умовами у векторі y, праві частини яких розташовані у символьному векторі F, на інтервалі від х1 до х2, де n – кількість кроків.}

_{rkfixed(y, x1, x2, n, F) – повертає матрицю рішень методом Рунге-Кутта систем звичайних диференційних рівнянь з початковими умовами у векторі y, праві частини яких розташовані у символьному векторі F, на інтервалі від х1 до х2 при фіксованій кількості кроків n.}

_{Розглянемо приклад рішення систем двух диференційних рівнянь с побудовою рішення у вигляді фазового портрета коливання, які описується рішенням заданої системи рівнянь.}

_{Рішення системи двух диференційних рівнянь методом Рунге-Кутта с фіксованим кроком}

Параметр системи

Вектор початкових значень

Система нелінійних

диференційних рівнянь

_{Завдання рішення}

Графік рішення у вигляді фазового портрета коливань

_{Рішення системи двух диференційних рівнянь адаптованим методом}

Параметр системи

Вектор початкових значень

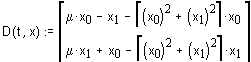
Система нелінійних

диференційних рівнянь

_{Завдання рішення}

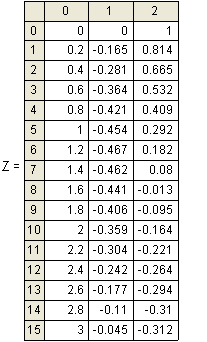
График рішенння у вигляді часових залежностей

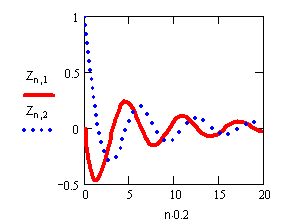
Функція Rkadapt зазвичай дає більш точний результат завдяки автоматичному зміненню кроку. Звичайно, по швидкості рахування вона програє rkfixed , хоч і не завжди – якщо рішення змінюється повільно, це може привести к помітному зменшенню кількості кроків. Таким чином, функція Rkadapt найбільш приваблива для розв’язання систем диференційних рівнянь, рішення яких повільно змінюються.