29.00.00 Физика
УДК 530.18 (УДК 530.10(075.4))
Яловенко
С.Н.
Харьковский Национальный
Университет Радиоэлектроники
Чёрный
предел. Часть 6.Электрический заряд
В приведенных выше главах заряд представлялся как диполь крептона (крепкая волна), который образуется в результате упаковки в квадратурный плоский водоворот и имеет форму спирали (рис.1). Срез спирали показана на рис.2 и 3.
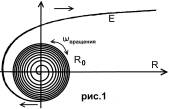
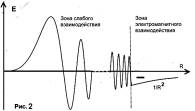

распределение заряда внутри водоворота для электрона и протона.
Если сделать срез посередине, то распределение заряда внутри водоворота от
![]() можно представить функцией
можно представить функцией
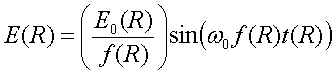
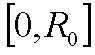
Здесь ![]() - функция
пропорциональности крептона при
- функция
пропорциональности крептона при ![]() , где
, где ![]() - средняя величина,
характеризующая плотность крептона (вакуума);
- средняя величина,
характеризующая плотность крептона (вакуума); ![]() - частота кванта
света,
- частота кванта
света, ![]()
![]() - амплитуда цуга ,
- амплитуда цуга , ![]() .- функция изменяющегося времени из-за изменении плотности крептона
при приближении к центру водоворота. Так, для водоворота вида
.- функция изменяющегося времени из-за изменении плотности крептона
при приближении к центру водоворота. Так, для водоворота вида ![]() при N=2
уравнение будет иметь вид
при N=2
уравнение будет иметь вид

![]()
В водоворотной
крептоновой теории, которая была представлена в шести предыдущих публикациях ,
все частицы а их (более тысячи) представлялись как плоские водовороты с
изменяющейся квадратурной плотностью (![]() ), крептоном в которой электромагнитная волна упаковывалась
определенным образом (свернутой в плоскую
спираль). Напряжённость электрического поля создаваемая каждой элементарной
частицей (электроном, протоном, нейтрино) была, плоской и составляло:
), крептоном в которой электромагнитная волна упаковывалась
определенным образом (свернутой в плоскую
спираль). Напряжённость электрического поля создаваемая каждой элементарной
частицей (электроном, протоном, нейтрино) была, плоской и составляло:
![]()
 (1)
(1)
 (2)
(2)
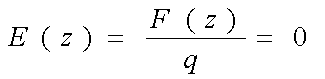 (3)
(3)
 (4)
(4)
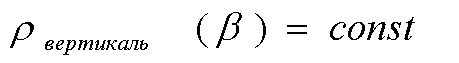 (5)
(5)
Где ![]() - напряженность электрического
поля (векторная величина),
характеризующая электрическое поле в данной точке. Ключевой момент водоворотной крептоновой теории заключается в
том, что мы состоим из плоскостей
создающих объем;
- напряженность электрического
поля (векторная величина),
характеризующая электрическое поле в данной точке. Ключевой момент водоворотной крептоновой теории заключается в
том, что мы состоим из плоскостей
создающих объем;
q – электрический заряд;
![]() - расстояние
от исследуемой точки пространства до центра заряда;
- расстояние
от исследуемой точки пространства до центра заряда;
![]() - вероятностное
расположение оси угла плоскости XY по горизонтали.
- вероятностное
расположение оси угла плоскости XY по горизонтали.
![]() - вероятностное
расположение оси угла плоскости XY по вертикали
- вероятностное
расположение оси угла плоскости XY по вертикали
Равновероятностное
и одинаковое распределение оси угла плоскости XY по
горизонтали и вертикали ![]() =
=![]() =const создает сферу одинакового равновероятностного воздействия электрической
силы и напряженности электрического поля. Статистически
по суммарному усреднению
=const создает сферу одинакового равновероятностного воздействия электрической
силы и напряженности электрического поля. Статистически
по суммарному усреднению
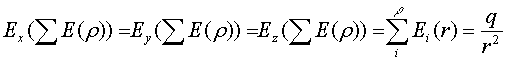 (6)
(6)
Однако только при условии равной вероятности углов вращения по горизонтали и вертикали , что реализуется, когда плоскости объектов расположены далеко друг от друга и их влиянием можно пренебречь.
Поэтому напряженности
![]() (7)
(7)
равны между собой, вследствие статистически равного вероятностного суммарного воздействия. По аналогии –вследствие равновероятностного воздействия давление на стенки сосуда с газом (или жидкостью) одинаково на всех стенках сосуда.
Поэтому напряжённость электрического поля представлена в виде суммы плоскостей напряженности электрического поля зарядов элементарных частиц и согласно уравнениям (1)-(5).
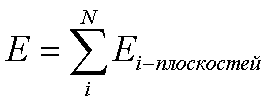
Как видно из
рис.2 , 3, область заряда, растянута квадратурным водоворотом.. Нарисуем и
рассмотрим эту часть подробнее. На рис.
4 показана синусоида ![]() SIN(x) на участке от
SIN(x) на участке от ![]() , которая свернута квадратурным водоворотом смотри (рис. 1).
На рис. 5. показана область синусоиды
, которая свернута квадратурным водоворотом смотри (рис. 1).
На рис. 5. показана область синусоиды ![]() или
или ![]() , которую квадратурный водоворот растягивает в заряд (рис. 6).,
то есть область
, которую квадратурный водоворот растягивает в заряд (рис. 6).,
то есть область ![]() или
или ![]() , переходит, или растягивается, водоворотом в область
, переходит, или растягивается, водоворотом в область ![]() пропорционально
пропорционально ![]() (или
(или ![]() ).
).



![]()
Как видно из графиков рис 4 ,5 ,6 и из водоворотной крептоновой (эфирной) теории. Сила между двумя зарядами, которая записывалась как
![]() (8)
(8)
и напряжённость электрического поля
![]() (9)
(9)
векторные физические величины, характеризующие электрическое поле в данной точке и численно равные отношению силы F действующей на пробный заряд, помещенный в данную точку поля, к величине этого заряда q.
Эти физические величины неточны.
В формулах (8) и (9) правильно поставить знак приближения (![]() ), и записать как
), и записать как


Правильная формула должна учитывать наложение синуса (SIN(x) ) растянутой функции (рис.7). Так как часть функции (SIN(x) ) скручивается в спираль а конец растягивается водоворотом – он то с отвечает за электрический заряд частицы.
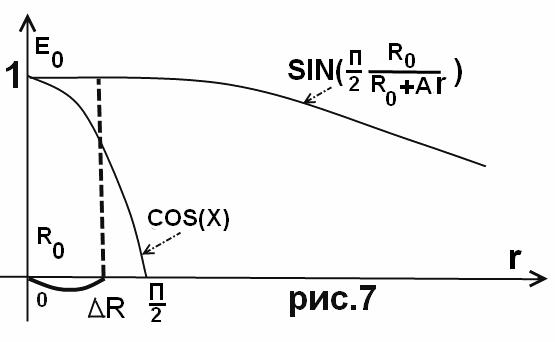
Формулы (8) и (9)
верны приближенно, так как на участке ![]() (рис.7). функция
(рис.7). функция ![]() .
.
Для нахождения
растянутой функции используем метод замены переменной в определённом интервале.
Где функции ![]() на промежутке
на промежутке ![]() соответствующей концу
водоворота преобразуется функцией
соответствующей концу
водоворота преобразуется функцией ![]() на интервал
на интервал ![]() . Тогда получим:
. Тогда получим:
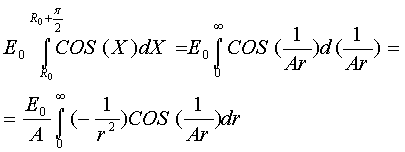
Перенесём для
упрощения ось ординат в ![]()
 (10)
(10)
Как видно из (рис.7) формулы (8) и (9) (10) нужно учитывать изменение заряда от расстояния r . То есть заря, есть функция от расстояния q(r) и выводится, и записывается как
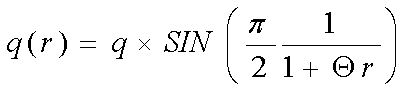 (11)
(11)
Точная формула, как следует из теории должна записываться как

 (12)
(12)
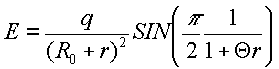
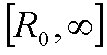 (13)
(13)
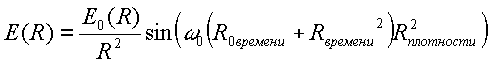
![]() (14)
(14)
Где 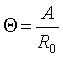 - коэффициент растяжения, зависящий от скорости света
среды
- коэффициент растяжения, зависящий от скорости света
среды ![]() .
.
Из уравнений
(12) и (13) можно видеть, что на небольших расстояниях (![]() ) где
) где ![]() функция
функция ![]() , а
, а ![]() <<
<<![]() и им можно
пренебречь и уравнения
(12),(13) переходят в уравнения (8)
и (9)
и им можно
пренебречь и уравнения
(12),(13) переходят в уравнения (8)
и (9)
![]() и
и
![]() .
.
Но на больших
расстояниях надо учитывать действие
распределенного заряда уравнение (11) или функцию распределения заряда в
пространстве;
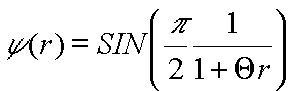 (15)
(15)
На больших
расстояниях функция ![]() , а
, а ![]() <<
<<![]() и им можно
пренебречь и уравнения (12),(13)
можно записать как
и им можно
пренебречь и уравнения (12),(13)
можно записать как
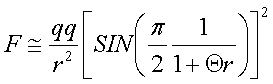 (16)
(16)
 (17)
(17)
Что существенно ограничивает действие заряда в пространстве по сравнению с гравитационной функцией. В данном случае формула заряда получается не экспериментальным путём, а выводится из теории. Аналогично будет сделано и для гравитации.
![]() (18)
(18)
Которая, (как будет показано дальше) тоже нуждается в уточнении.
В водоворотной теории заряд рассматривается как дипольное смещение крепнтона (элемента эфира) (рис.8). На (рис.9) крептон изображён без смещения (нейтральный).
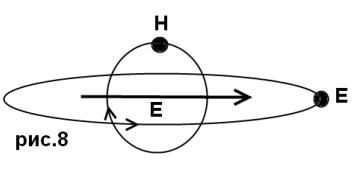

На этих рисунках приведены также обозначения :
Н –крептонит, отвечающий за магнитную составляющую;
Е – крептонит, отвечающий за электрическую составляющую.
Сила взаимодействие
между условными шариками крептонам Н и крептонам Е происходит по аналогии силы Лоренца, и направления их движения перпендикулярны друг другу, вследствие чего
их орбиты также перпендикулярны друг другу![]() . Об устройстве
крептонитов Е и Н и почему они обладают такими свойствами, будет описано в
последующих главах. Все уравнения представлены в декартовой системе координат
для наглядности и простоты, но в дальнейшем для точности будут записаны в
полярных координатах.
. Об устройстве
крептонитов Е и Н и почему они обладают такими свойствами, будет описано в
последующих главах. Все уравнения представлены в декартовой системе координат
для наглядности и простоты, но в дальнейшем для точности будут записаны в
полярных координатах.
Список
используемой литературы
1. А. Эйнштейн. Теория относительности. 2000 Научно-издательский центр. Регулярная и хаотическая динамика
2. Фейнман Р., Лейтон Р., Сэндс М. - Фейнмановские лекции по физике.
3. Яловенко С.Н., Материалы Международной научно-практической конференции. «Актуальные проблемы современных наук-2009» №.21.издат. «Nauka I studia;2009».ISBN 978-966-8736-05-6. Чёрный предел. Теория относительности: новый взгляд., стр. 85
4. Яловенко С.Н. Уральский научный вестник. Научно-теоретический и практический журнал. №5(20) 2009. ЖШС «Уралнаучкнига» 2009. ISSN 1561-6908 , Теория относительности .Новый взгляд. стр. 33
5. Яловенко С.Н. Вестник национального технического университета "ХПИ" №8 2009г Тематический выпуск «Новые решения в современных технологиях»; Чёрный предел. Харьков., 2009 г. стр.81
6.
Яловенко С.Н.
Вестник национального технического университета "ХПИ" №43 2008г
Тематический выпуск «Новые решения в современных технологиях»; Чёрный предел
часть 1 Харьков., 2008 г. стр.144
7. Яловенко С.Н. «Чёрный предел. Теория относительности: новый взгляд» ТОВ издательство «Форт» 2009г. ISBN 978-966-8599-51-4
8. Яловенко С.Н., Материалы 6 Международной научно-практической конференции. «Наука и инновации - 2010» №.13. Techniczne nauki Fizyka .издает. «Nauka I studia;2010».ISBN 978-966-8736-05-6. Чёрный предел. Теория относительности: новый взгляд. Часть 5. Мировоззрение, стр. 105
9.
Яловенко С.Н.,
Материалы 6 Международной научно-практической конференции. «Наука : Теория и
практика - 2010» №.7. издает. «Nauka I studia;2010».ISBN 978-966-8736-05-6.
Чёрный предел. Теория относительности: новый взгляд, стр. 78
10.
Yаlovenko S.N., Научно-теоретический и
практический журнал. «Современный научный вестник №21 (77) 2009» ISSN
1561-6886 ФИЗИКА. Black limit. Theory of relativity. New view.
Стр.67.
11.
Yаlovenko S.N., Материалы 6
Международной научно-практической конференции. «Наука: Теория и практика» №.6. издает.
«Nauka
I studia;2009».ISBN 978-966-8736-05-6.раздел.
Fizyka. Teoretyczna fizyka. Black
limit. Theory of relativity. New view. Стр.17.
12.
Yаlovenko S.N., Материалы 6 Международной научно-практической конференции.
«Научный прогресс на рубеже тысячелетий - 2010» от 27.05.2010 – 05.06.2010г. издает.
Прага«Education and Science».
ISBN 978-966-8736-05-6.
Continuation of the theory of a relativity. стр. 10.
530.1
Ф 50
УДК 530.18 (УДК 530.10(075.4)) Яловенко С.М. Чёрный предел. Часть 6. Заряд
Розглянуто заряд точки зору коловоротної та дискретної (криптонової) теорії.
Э-534
ISBN 5-93972-002-1
530.1
Ф 50
УДК 530.18 (УДК 530.10(075.4)) Яловенко С.Н. Чёрный предел. Часть 6. Заряд
Рассмотрен электрический заряд с точки зрения водоворотной и дискретной (криптоновой) теории.
Э-534
ISBN 5-93972-002-1
530.1
Ф 50
УДК 530.18 (УДК 530.10(075.4)) Yalovenko S.N
Black
a limit. A part 6. A
charge
The electric charge from the point
of view водоворотной
and discrete (the krypton ) theories is considered.
ISBN 5-93972-002-1