Технические науки/ 2.Механика

¹Д.ф.-м.н. Тюреходжаев А.Н., ²к.ф.-м.н. Рыстыгулова В.Б.

¹Казахский национальный технический университет имени К.И. Сатпаева,

²Казахский национальный педагогический университет имени Абая, Казахстан

ОСЕСИММЕТРИЧНАЯ ДЕФОРМАЦИЯ

ЦИЛИНДРИЧЕСКОЙ ОБОЛОЧКИ

В работе [1] разрешающие уравнения для осесимметричной задачи тонкостенной цилиндрической оболочки сводится к одному в связи с введением комплексной переменной. При этом получено частное решение соответствующий безмоментному состоянию цилиндрической оболочки для плавного изменения нагрузки допуская некоторые и другие ограничения. В настоящей работе система неоднородных дифференциальных уравнений решается методом частичной дискретизации нелинейных уравнений [2] без каких-либо упрощении.

Тонкостенные оболочки имеет важное практическое значение в машиностроении, авиастроении, ракетостроении, судостроении и во многих других областях.

Рассматривается тонкая цилиндрическая оболочка, при этом один край оболочки предполагается закрепленным, другой – свободным. Оболочка деформируется под действием распределенной нагрузки. Система разрешающих уравнений при осесимметричном нагружении имеет вид

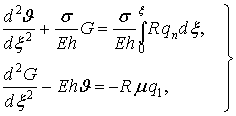(1)

где угол поворота, силовая функция, составляющие распределенной нагрузки, модуль упругости, - параметр, характеризующий относительную толщину оболочки, радиус и толщина сферы, коэффициент Пуассона, безразмерная координата, причем ; сечение и высота цилиндра.

Граничные условия запишутся в виде

1) при (2)

2) при

где радиальное перемещение, радиальное усилие, меридиональный изгибающий момент.

Приведенные граничные условия, записанные через функции и дают

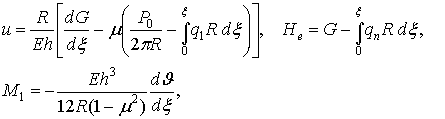(3)

где постоянная интегрирования, равная осевому усилию в крайнем сечении .

Дискретизируя в первом уравнении (1) функцию , и подставляя ее во второе уравнение, получим общее решение

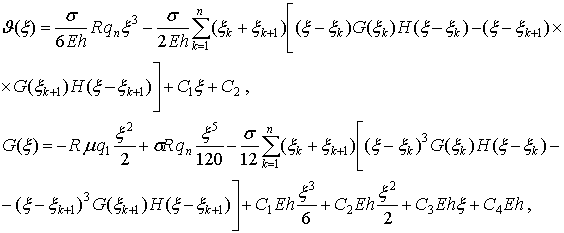(4)

где единичная функция Хевисайда.

Решение системы (1), соответствующее граничным условиям (2) примут вид

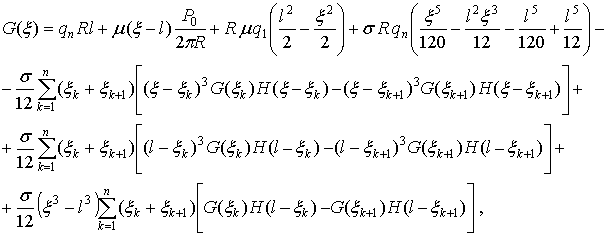(5)

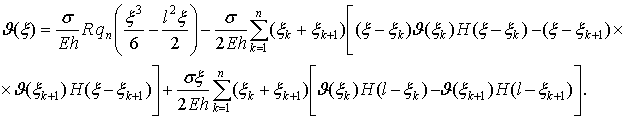
Приведем график угла поворота срединной поверхности цилиндрической оболочки от безразмерной координаты при нагрузках . Материал оболочки сталь и , толщина и радиус оболочки см, см, высота цилиндра см. Для расчета использована программа MathCad.

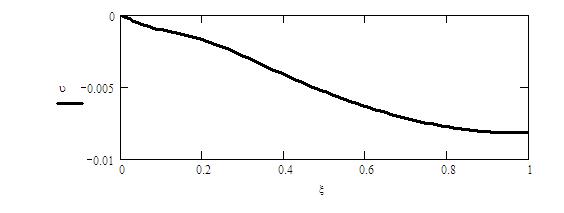
Рис.1. Зависимость угла поворота от

Силовые характеристики цилиндрической оболочки выражаются через силовую функцию и угол поворота по формулам

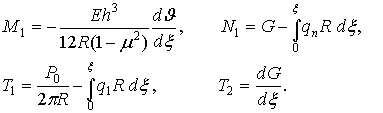(6)

Получены выражения закономерностей изменения усилий и изгибающих моментов для моментной теории изгиба цилиндрической оболочки:

,

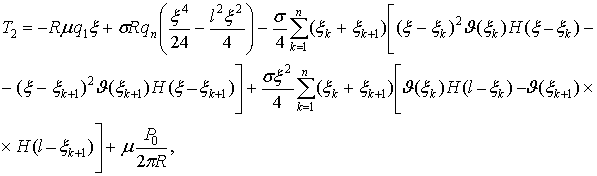
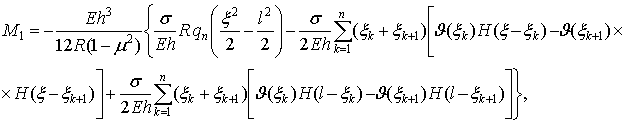
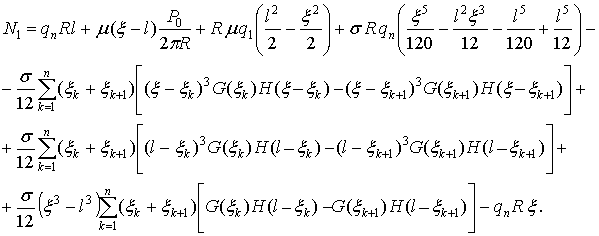
Работа выполнена в рамках научной программы по фундаментальным исследованиям МОН РК «Решение актуальных прикладных задач механики твердого и деформируемого твердого тела методами Каппа-функции, частичной дискретизации нелинейных дифференциальных уравнений и непрямым операторным» (УДК 539.3; 531.3 № госрегистрации: 0109РК00669).

Литература

1. Чернина В.С. Статика тонкостенных оболочек вращения. Главная редакция физико-математической литературы издательства «Наука», 1968, 456 с.

2. Тюреходжаев А.Н., Рыстыгулова В.Б. Изгиб составной неоднородной кольцевой пластины // Сборник докладов VII Международной конференции «Проблемы прочности материалов и сооружений на транспорте», 23-24 апреля 2008 г., Санкт-Петербург. С.260-266. ISBN 978-5-7641-0212-2