Бондаренко Л. Н., Матвиец Т. В., Бондаренко В. Д., Ильенко К.И.

Приднепровская государственная академия строительства и архитектуры

Квазистатика математического маятника с реальным шарниром

При определении натяжения нерастяжимой и невесомой нити математического маятника традиционно считается, что нить подвешена к неподвижной точке, т.е. шарнир является идеальным. Естественно, что на практике такой шарнир невозможен. Теоретически возможно неограниченное количество видов шарниров, но здесь мы рассмотрим только два.

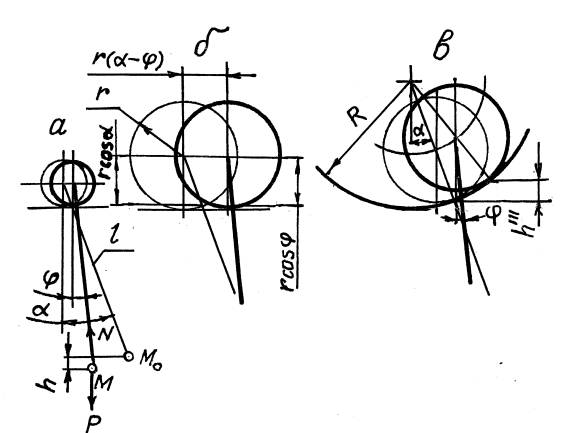
Рис. 1. Математический маятник с опиранием шарнира на плоскость

В первом случае шарнир маятника радиусом опирается на плоскость. Найдем угловую скорость маятника в тот момент, когда нить ОМ образует с вертикалью угол (рис.1). Трением качения шарнира по плоскости будем пренебрегать.

Если начальное положение точки М обозначить через М₀, то работа сил тяжести на пути М₀ – М будет равна Ph, где - вертикальное перемещение груза (рис.1), где - вертикальное перемещение груза маятника при идеальном шарнире; - то же перемещение за счет шарнира.

Согласно закона об кинематической энергии из рис. 1 нетяжело доказать, что

(1)

Или

(2)

Если угловую скорость маятника обозначить через , то

. (3)

В момент прохождения маятника через, например, вертикальное положение будем иметь

. (4)

Определим натяжение нити в момент, когда маятник образует с вертикалью угол . Оно численно равно реакции нити , а для ее определения воспользуемся методом кинетостатики. Присоединим к силам и центробежную силу инерции , тогда получим систему сил, находящихся в равновесии. Сумма проекций этих сил на любое направление должна быть равна нулю. Спроектировав на направление ОМ, получим

, (5)

откуда

. (6)

Но поскольку

,

то на основании уравнения (1)

(7)

Теперь , а в момент прохождения маятника через вертикального положение (

(8)

и зависит от радиуса шарнира маятника в отличие от идеального шарнира [1].

Рассмотрим случай, когда шарнир основания выполнен в виде цилиндра радиусом (рис. 1в). В этом случае , где и величина определится из выражения

. (9)

Если в выводы для предыдущего случая вместо подставить выражение (9), то получим формулы по структуре близкими к полученным, но содержащими дополнительно , показывающий отклонение от вертикали, проходящей через центр неподвижного шарнира.

В заключении отметим, что введение в расчет математического маятника вместо идеального шарнира реального по геометрии приводит к изменению как угловой скорости маятника, так и натяжения нити.

Литература:

1. Николаи Е.Л. Теоретическая механика. Ч. II. М.: Гостехиздат, 1956. 484с. (задача на стр.56)