Технічні науки / галузеве машинобудування
Скачков В.О., Іванов В.І., Воденнікова О.С., Мосейко Ю.В.
МОДЕЛЮВАННЯ
ІзотермІЧНОГО УЩІЛЬНЮВАННЯ ВУГЛЕЦЕВИХ КОМПОЗИТІВ ІЗ ГАЗОВОЙ ФАЗИ
Запорізька державна інженерна
академія
У
технології виробництва вуглецевих композитних матеріалів одним з важливих
переділів є ущільнення пористої структури карбонізованого вуглепластика з
газової фази з використанням природного газу.
У обсязі ізотермічного реактора проточного типу відбувається піролиз метану з
утворенням радикалів, вуглеводнів і сажистого вуглецю. На всіх нагрітих
поверхнях вуглепластика відбуваються гетерогенні реакції з осадженням твердої
фази – піролітичного вуглецю.
За умов руху газових потоків уздовж осі реактора та малої швидкості дифузії
порівняно із швидкістю руху потоків рівняння перенесення маси i-того реагуючого компоненту суміші реакційних газів
приймає вигляд:
![]() , (1)
, (1)
де U – швидкість газового потоку на осі
реактора; Сi –
концентрація i-того реагуючого компоненту в обсязі
реактора; z – координата на осі
реактора; ![]() – швидкість хімічного перетворення i-того реагуючого
компоненту; i – номер реагуючого
компоненту
– швидкість хімічного перетворення i-того реагуючого
компоненту; i – номер реагуючого
компоненту
 ;
;
b – константа швидкості дифузії; ![]() – константа швидкості
гетерогенної реакції i-того
реагуючого компоненту на поверхні ущільнюваного
вуглепластика S;
– константа швидкості
гетерогенної реакції i-того
реагуючого компоненту на поверхні ущільнюваного
вуглепластика S; ![]() – концентрація i-того компоненту на поверхні
вуглепластика S; R –
радіус реактора; wп –
відносна пористість поверхні матеріалу вуглепластика; Di – коефіцієнт дифузії i-того реагуючого
компоненту; r – радіус пори.
– концентрація i-того компоненту на поверхні
вуглепластика S; R –
радіус реактора; wп –
відносна пористість поверхні матеріалу вуглепластика; Di – коефіцієнт дифузії i-того реагуючого
компоненту; r – радіус пори.
Вважають,
що під час реалізації процесів ущільнення пористої структури виконуються такі
умови: швидкість осадження піровуглецю
в пористій структурі ущільнюваного вуглепластика є достатньо малою; пористість
ущільнюваного вуглепластика є функцією часу, що поволі змінюється.
В такому разі
задачу щодо масопереносу в одиничній циліндровій порі карбонізованого
вуглепластика можна записати:
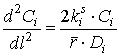 (2)
(2)
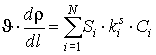 (3)
(3)
![]() (4)
(4)
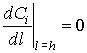 (5)
(5)
![]() , (6)
, (6)
де ![]() , l – середній радіус і глибина пори
відповідно; 2h – товщина виробу; Si –
питома реакційна поверхня композиту; r0 –
початкова щільність матеріалу композиту;
J –
швидкість зростання піролітичного вуглецю;
N – кількість реагуючих компонентів в обсязі реактора.
, l – середній радіус і глибина пори
відповідно; 2h – товщина виробу; Si –
питома реакційна поверхня композиту; r0 –
початкова щільність матеріалу композиту;
J –
швидкість зростання піролітичного вуглецю;
N – кількість реагуючих компонентів в обсязі реактора.
Вирішення диференційного рівняння (2) з урахуванням умов (3)…(6) можна подати
у вигляді співвідношень:
 , (7)
, (7)
де ![]() – початкова
концентрація i-того реагуючого
компоненту;
– початкова
концентрація i-того реагуючого
компоненту; 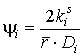 .
.
У зв’язку з тим, що величина питомої реакційної поверхні карбонізованого
вуглепластика Si відповідає питомій поверхні пор,
її можна визначити за співвідношенням:
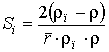 , (8)
, (8)
де rп –
дійсна щільність матеріалу карбонізованого вуглепластика.
Після
підставляння співідношення (8) до диференційного рівняння (2) з урахуванням
співвідношення  матимемо:
матимемо:
 (9)
(9)
Подальше
інтегрування рівняння (9) за r (у межах від r0 до
r)
і за l (у межах від 0 до l) дозволяє одержати трансцендентне
рівняння щодо параметра, що характеризує змінювання щільності матеріалу, яка
здається, для вуглепластика за товщиною стінки виробу:
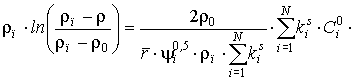
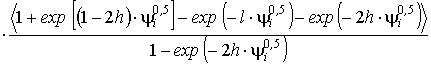 . (10)
. (10)
Для реалізації обчислювального експерименту на ПЕОМ з використанням
запропонованої математичної моделі розроблено комп’ютерну програму на
алгоритмічній мові TURBO-PASKAL.
Ідентифікацію математичної
моделі (10) проводили шляхом порівняння розрахункових значень щільності карбонізованого вуглепластика з
фактичними даними, одержаними під час проведення оптико-механічних досліджень.
Розбіжність теоретичних та експериментальних значень щільності не перевищує 0,6
%.