Костоглотов А.А., Кузнецов А.А., Скрипкин И.Г.

Военный авиационный инженерный университет, Россия

Интеллектуальный алгоритм идентификации параметров

информационно-измерительных систем

Известно, что для повышения точности измерений информационно-измерительных систем (ИИС) необходимо решать задачу одновременной идентификации параметров объекта измерений и параметров первичных измерительных преобразователей ИИС [1].

Существующие алгоритмы идентификации ИИС, построенные на базе классических методов статистического синтеза, в условиях априорной неопределенности не всегда обеспечивают получение требуемой точности сходящихся оценок искомых параметров [2]. Под априорной неопределенностью в рамках данной работы понимаются условия, при которых значения параметров компонентов ИИС отклоняются от номинальных значений и характер внешних воздействий неизвестен.

В сложившейся ситуации задача синтеза алгоритмов идентификации, обеспечивающих в условиях априорной неопределенности получение сходящихся высокоточных оценок измеряемых ИИС параметров и параметров компонентов ИИС, весьма актуальна.

Помимо известных подходов к синтезу алгоритмов идентификации, основанных на классических методах обработки информации, существуют подходы, основанные на: стохастической аппроксимации; принципе регуляризации [3]; концепции обратных задач динамики [4]. Из перечисленных подходов наиболее перспективным представляется подход, основанный на принципе регуляризации, поскольку задача идентификации параметров относится к обратным задачам, которые, как правило, являются некорректно поставленными.

Пусть динамика контролируемых ИИС параметров описывается системой уравнений первого порядка

(1)

где x(t) - вектор параметров, неизвестное внешнее возмущение, - переходная функция системы, непрерывная вместе с производными по совокупности переменных.

Уравнение наблюдения имеет вид

(2)

где сигнальная функция непрерывная по совокупности переменных, - вектор белого гауссовского шума с известными локальными характеристиками, - векторная дельта-функция.

Ставится задача синтеза алгоритма получения оценки , оптимальной в смысле минимума неотрицательного функционала

. (3)

В силу непрерывности переходной функции решения уравнения (1) непрерывно зависят от [5]. Поэтому задача определения оценки , доставляющей минимум (3), равносильна задаче определения

(4)

Задача (1),(2),(4) согласно [3] является некорректно поставленной и относится к задачам типа оптимального управления. Решение данной задачи с использованием метода регуляризации А.Н.Тихонова [3] и градиентных методов [6] представлено в работе [7]. При решении использован сглаживающий функционал

, (5)

где - стабилизирующий функционал [3], - параметр регуляризации, который традиционно [3,8] для обеспечения сходимости и устойчивости подчинен условиям

< ∞. (6)

В результате решения задачи (1),(2),(4) получена система уравнений итеративного алгоритма идентификации

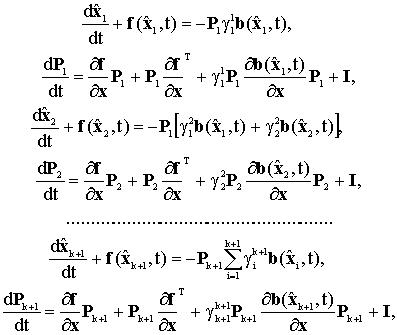(7)

где ; I – единичная матрица.

Жесткое задание параметра не учитывает характер внешних воздействий. Для получения интеллектуального алгоритма, способного адаптироваться к внешним воздействиям, необходимо согласовать значения получаемых параметров регуляризации с измерительной информацией. Это достигается путем определения параметра регуляризации с использованием градиентных методов при условии минимума функционала невязки (3). В работе [7] представлено выражение для параметра регуляризации, полученное с использованием метода минимальных ошибок

. (8)

Система уравнений (7) в совокупности с (8) представляет собой интеллектуальный алгоритм идентификации на основе метода минимальных ошибок,

Интеллектуальность алгоритма заключается в определении связи между значением параметра регуляризации и текущей измерительной информацией.

Для определения свойств разработанного алгоритма было проведено численное моделирование в среде MathCAD 11. Синтезированный алгоритм использовался для решения задачи определения неизвестного параметра =0,2, определяемого конструктивными особенностями первичных измерительных преобразователей ИИС, описываемых дифференциальным уравнением

,

по результатам наблюдения при наличии внешних воздействий и ошибок измерений.

Результаты моделирования представлены на рис. 1 в виде графиков оценок ,,,, идентифицируемого параметра . Где - оценка фильтра Калмана-Бьюси, , – второй и третьей итераций алгоритма (7) с вручную подобранными параметрами регуляризации, , – второй и третьей итераций алгоритма на основе метода минимальных ошибок.

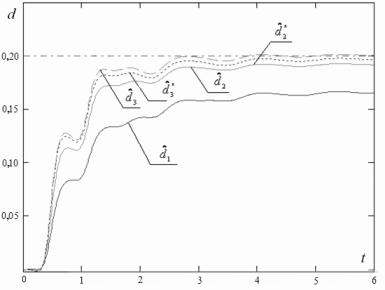
Рисунок 1

По результатам проведенного численного моделирования было установлено, что разработанный алгоритм превосходит по точности получаемых оценок на 10-15% фильтр Калмана-Бьюси, а также устойчив к повышению уровня внешних воздействий и шумов каналов ИИС.

Литература:

1. Ранеев Г.Г. и др. Информационно-измерительная техника и технологии – М.: Высшая школа, 2002.

2. Фарина А., Студер Ф. Цифровая обработка радиолокационной информации. Сопровождение целей. – М.: Радио и связь. 1993.

3. Тихонов А.Н., Арсенин В.Я. Методы решения некорректных задач. – М.: Наука. 1986.

4. Костоглотов А.А. Метод синтеза оптимального алгоритма угловой стабилизации на основе объединенного принципа максимума. // Автоматика и вычислительная техника. 2002. №5. С.26-34.

5. Карташев А.П., Рождественский Б.Л. Обыкновенные дифференциальные уравнения и основы вариационного исчисления. – М.: Наука, 1986.

6. Алифанов О.М., Артюхин Е.А., Румянцев С.В. Экстремальные методы решения некорректных задач. - М.: Наука, 1988.

7. Костоглотов А.А., Кузнецов А.А. Синтез интеллектуальной измерительной процедуры на основе метода минимальных ошибок. // Измерительная техника. 2005. №7. С.8-13.

8. Детистов В.А., Таран В.Н. Синтез оптимального управления градиентным методом на основе прогнозирующей модели. //Автоматика и телемеханика. 1990. №10. С.45-56.