Функциональное уравнение,
возникающее при восстановлении метрики по
группе движений пространства Евклида
В данной работе методом
решения функциональных уравнений решается задача о восстановлении метрики по
группе движений пространства Евклида.
Ключевые
слова: пространство Евклида,
группа движений, метрическая функция, функциональное уравнение.
Рассмотрим пространство
Евклида с метрической функцией (квадрат метрики) [1]
(1)
Как известно, метрическая функция
(1) сохраняется относительно преобразований шестипараметрической локальной
группы движений, то есть таких гладких и обратимых преобразований [2]:
для которых:
(2)
где, например, 
. Заметим, что якобиан 
. Таким образом, метрическая функция является
двухточечным инвариантом группы движений.
Рассмотрим проблему
восстановления метрической функции пространства Евклида по группе движений. Эта
задача сводится к решению функционального уравнения (2) при неизвестной
метрической функции и известных уравнений группы движений. Эти уравнения
возьмем в виде:
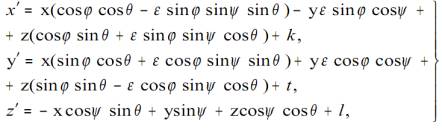
Уравнение (2) как функциональное
уравнение относительно метрической функции (1) тогда запишется так:
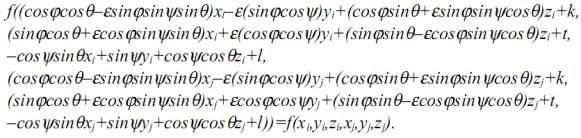
Дифференцируя,
данное уравнение по параметрам k, t, l, φ, ψ и θ,
а затем в полученных дифференциальных соотношениях придавая значения, соответствующие
тождественному преобразованию: φ =0, ψ
=0, θ =0, k=0, t=0, l=0, ε=1, получим систему шести
линейных однородных дифференциальных уравнений в частных производных (3):
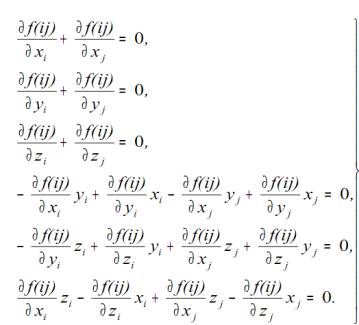
(3)
Решая исходную систему
дифференциальных уравнений, находим невырожденный двухточечный инвариант f(ij):
который эквивалентен метрической
функции пространства Евклида (1), переходящей в него при масштабном
преобразовании 
.
Литература:
1. Дубровин Б.А., Новиков С.П., Фоменко А.Т. Современная
геометрия. М.: -Наука, 1979г.
2. Михайличенко Г.Г. Двумерные геометрии. Барнаул: -
Барнаульский государственный педагогический университет, 2004, 132 с.