Е.И. Ермолаева

Метод наименьших квадратов в математическом моделировании

В развитии различных областей человеческой деятельности математика оказывает и оказывала существенное влияние. Современное развитие науки характеризуется потребностью изучения всевозможных сложных процессов и явлений – физических, химических, биологических, экономических, социальных и других. Происходит значительное увеличение темпов математизации и расширение ее области действия - особую роль при этом играет математическое моделирование. Математической моделью называется совокупность математических соотношений, уравнений, неравенств и т.п., описывающих основные закономерности, присущие изучаемому процессу, объекту или системе.

Математическая модель, основанная на упрощении, идеализации, не тождественна реальному явлению, объекту, а является его приближенным описанием. Однако благодаря замене реального объекта приближенной моделью становится возможным его математическое описание и применение математического аппарата для его анализа. Математика позволяет провести детальный анализ рассматриваемого явления, предсказать его поведение в различных условиях и в будущем.

При обработке экспериментальных данных часто приходится представлять их в виде некоторой приближенной зависимости типа . Задача формулируется следующим образом. Пусть в результате измерений получена таблица данных:

			…
			…

Необходимо построить зависимость , приближенно отображающую эти данные. Эта зависимость называется эмпирической формулой. Математическое моделирование задач различных областей науки легко приводит именно к этой зависимости. Причем вид эмпирической формулы может быть произвольным. В этом случае предпочтение отдается наиболее простым формулам, обладающим достаточной точностью. Вид их первоначально можно выбрать из геометрических соображений. Одним из методов определения параметров эмпирической формулы является метод наименьших квадратов. Он широко применяется на практике и обеспечивает приемлемую точность. Построение математической модели при нем может иметь несколько вариантов.

Пример: Проводится исследование спроса на некоторый вид товара. Пробные продажи показали следующие данные о зависимости дневного спроса от цены:

Цена, руб. (x)	10	12	14	16	18
Спрос, шт. (y)	91	76	68	59	53

Требуется: выбрав в качестве эмпирической формулы прямую, определить ее параметры методом наименьших квадратов; выбрав в качестве эмпирической формулы модель зависимости спроса от цены: , определить параметры указанной формулы методом наименьших квадратов и сделать вывод о том, какая модель является более адекватной экспериментальным данным.

Решение.

1. Запишем сумму квадратов отклонений для всех точек :

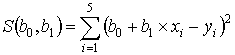
Минимум функции определим, приравняв к нулю частные производные по переменным и . В результате имеем систему:

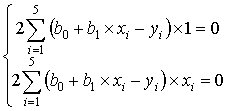
После преобразований имеем:

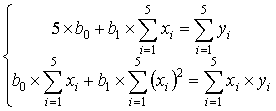
Для решения данной системы заполним следующую таблицу

	x	y	X^2	xy
	10	91	100	910	88	-3	9
	12	76	144	912	79	3	9
	14	68	196	952	69	1	1
	16	59	256	944	60	1	1
	18	53	324	954	51	-2	4
Итого:	70	347	1020	4672	—	—	24

В результате имеем систему:

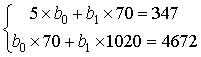
Решив ее, имеем: , .

Таким образом, линейная модель данного эксперимента выглядит следующим образом:

Подставив в это уравнение цену x, заполняем столбец таблицы. Это будет теоретический спрос, определенный по эмпирической формуле.

Далее заполняем столбец , где определяем разницу между теоретическим спросом и реальным . После этого возводим эту разницу в квадрат и заполняем столбец таблицы.

Определяем ошибку данного вычисления:

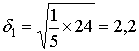
2. Выберем в качестве модели гиперболу и определим ее параметры методом наименьших квадратов.

Обозначим . Тогда имеем

Это линейная модель, поэтому неизвестные параметры и определим, решив систему уравнений

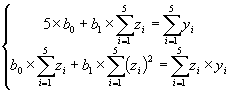
Для решения данной системы уравнений заполним следующую таблицу

	x	y	Z	z^2	zy
	10	91	0,1000	0,01	9,1000	91	0	0
	12	76	0,0833	0,006944	6,3333	77	1	1
	14	68	0,0714	0,005102	4,8571	67	-1	1
	16	59	0,0625	0,003906	3,6875	59	0	0
	18	53	0,0556	0,003086	2,9444	53	0	0
Итого:	70	347	0,3728	0,029039	26,9224	—	—	2

В результате имеем систему:

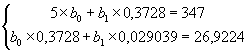
Решив ее, имеем: , .

Таким образом, модель данного процесса выглядит следующим образом:

Заполняем столбцы , , так же, как и в первом случае с линейной моделью. После этого определяем ошибку данного метода вычисления:

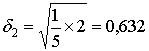
Вывод: таким образом, модель в виде гиперболы лучше отображает экспериментальные данные, чем линейная модель, так как для нее погрешность вычисления меньше .

Таким образом, построить математическую модель любой задачи при определенном методе возможно не единственным образом, и всегда возможен более оптимальный ход решения, мы рассмотрели это на примере использования метода наименьших квадратов.