Хасанов Ю.Х. (Душанбе, Таджикистан)
yukhas60@mail.ru
Об абсолютной
суммируемости кратных рядов Фурье
в терминах поведения
их коэффициентов Фурье
Пусть ![]() - линейное пространство, состоящее из функций
- линейное пространство, состоящее из функций ![]() , для которых
, для которых ![]() интегрируема по
Лебегу на любом к- мерном кубе пространства
интегрируема по
Лебегу на любом к- мерном кубе пространства ![]() и удовлетворяет
условию
и удовлетворяет
условию
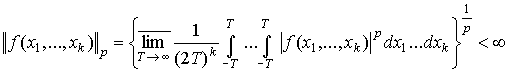 , (1)
, (1)
а при ![]()
![]() .
.
Следуя А.Безиковичу [1], при любом ![]() введем следующее определение
введем следующее определение ![]() - почти-периодической функции.
- почти-периодической функции.
Определение 1. Функцию ![]() будем называть
будем называть ![]() - почти-периодической, или почти-периодической в смысле Безиковича
(
- почти-периодической, или почти-периодической в смысле Безиковича
(![]() ), если:
), если:
1. ![]() измерима и
интегрируема в смысле Лебега на любом k – мерном
кубе пространства
измерима и
интегрируема в смысле Лебега на любом k – мерном
кубе пространства ![]() ;
;
2. 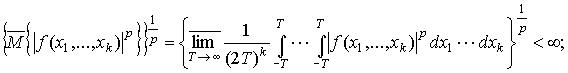
3. Существует
последовательность тригонометрических сумм
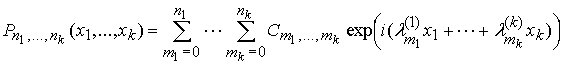 ,
,
для которой
![]()
Пространство функций ![]() , удовлетворяющих всем условиям определения 1 будем называть
, удовлетворяющих всем условиям определения 1 будем называть ![]() - пространством, или
- пространством, или ![]() – мерным пространством
Безиковича, в котором за норму функции
– мерным пространством
Безиковича, в котором за норму функции ![]() принимается величина (1).
принимается величина (1).
Для каждой функции ![]() рассмотрим при
фиксированном
рассмотрим при
фиксированном ![]() множество тех
множество тех ![]() , для которых
, для которых
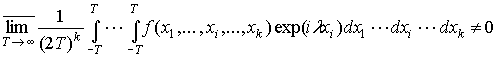 .
.
Множество таких ![]() является счетным.
Обозначим его через
является счетным.
Обозначим его через 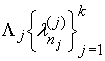 и назовем спектром
функции
и назовем спектром
функции ![]() по переменной
по переменной ![]() .
.
Для каждой функции ![]() можно поставить в соответствие
ее кратный ряд Фурье
можно поставить в соответствие
ее кратный ряд Фурье
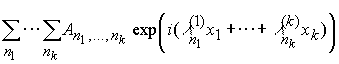 (2)
(2)
где
![]()
- коэффициенты Фурье функции ![]() .
.
В случае, когда какие-либо из ![]() по всем
по всем ![]() ряд (2) превращается
в ряд Фурье функции
ряд (2) превращается
в ряд Фурье функции ![]() лишь по тем
переменным, для которых хотя бы одно из
лишь по тем
переменным, для которых хотя бы одно из ![]() .
.
Определение
2. Кратный ряд 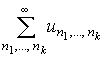 называется
называется ![]() - суммируемым
- суммируемым ![]() , если для любой совокупности индексов
, если для любой совокупности индексов
![]() выполнены условия
выполнены условия
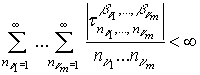 ,
,
где
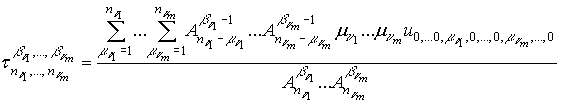 ,
,
![]() ,
,
и ![]() (m – число
индексов
(m – число
индексов ![]() , равных нулю);
, равных нулю);
Теперь устанавливаем ряд утверждений,
дающих критерии абсолютной чезаровской суммируемости кратного ряда Фурье
функции ![]() в терминах поведения их коэффициентов Фурье.
в терминах поведения их коэффициентов Фурье.
Теорема 1. Пусть ![]() и если
выполнены условия
и если
выполнены условия
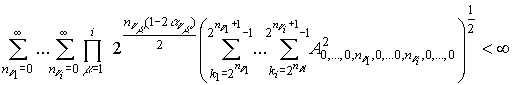 ,
,
где ![]() при любом
при любом ![]() , то ряд Фурье функции
, то ряд Фурье функции ![]() почти всюду
почти всюду ![]() - суммируем.
- суммируем.
Теорема
2. Пусть ![]() . Если выполнены условия
. Если выполнены условия
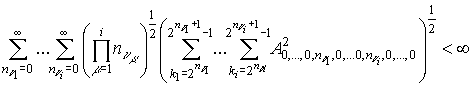 ,
,
то ряд Фурье
функции ![]() почти всюду
почти всюду 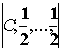 - суммируем.
- суммируем.
Теорема
3. Пусть ![]() и если
выполнены условия
и если
выполнены условия
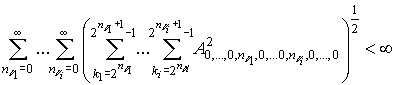 ,
,
где ![]() при любом
при любом ![]() , то ряд Фурье функции
, то ряд Фурье функции ![]() почти всюду
почти всюду ![]() - суммируем.
- суммируем.
Теоремы 1-3 являются обобщением результатов
Л.Лейндлера [2], в случае ![]() . Частный случай
результатов Лейндлера, соответствующий
. Частный случай
результатов Лейндлера, соответствующий ![]() - суммируемости почти
всюду ряда Фурье, был установлен в работе К.Тандори [3]. Для функций
- суммируемости почти
всюду ряда Фурье, был установлен в работе К.Тандори [3]. Для функций ![]() аналогичные
утверждения были получены в работах [4] и [5], а когда
аналогичные
утверждения были получены в работах [4] и [5], а когда ![]() , в работе [6].
, в работе [6].
ЛИТЕРАТУРА
1. Besicovitch A.S.
Almost periodic functions. Cambridge, 1932.
2. Leindler L. Uber
die absolute summierbarkeit der orthogonalreihen // Acta sci. math., (Szeged),
1961, 22, s. 243-268.
3. Tandori K. Uber die
orthogonalen functionen IX (Absolute summation) // Acta sci. math., 1960, 21, №
3-4, s. 292-299.
4.
Пономаренко Ю.А.
Некоторые критерии абсолютной чезаровской суммируемости кратных рядов Фурье //
Доклады АН СССР, 1963, 152, №6, с. 1305-1307.
5.
Пономаренко Ю.А., Тиман
М.Ф. Про абсолютну сумацiю кратних рядiв Фур'е // Украинский матем. журнал, 1971, 23, № 3, с.
346-363.
6.
Тиман М.Ф., Хасанов Ю.Х.
Об абсолютной суммируемости рядов Фурье некоторых классов почти-периодических
функций // Украинский математический журнал. № 9, 2009, с. 1267-1276.