Алмухамбетов С.С., Алмухамбетова Н.С.

Жетысуский Государственный университет им.И.Жансугурова

г.Талдыкорган., Республика Казахстана

Определение критической скорости движения и частот поперечных колебаний лент

Рассмотрим как влияет на величину критической скорости движения ленты и на частоту поперечных колебаний поперечная жесткость ленты на изгиб[1]. Линейное решение определяется из уравнения (1.19): L₀V₀= , (1.32)

Применяя метод Галеркина для получения V₀ и ω₀ , приходим к системе не связанных между собой алгебраических уравнений

(при m=1.2……N) (1.33)

Не связанные между собой алгебраические уравнения могут появиться только при нулевой скорости переноса. Линейное фундаментальное решение имеет вид:

V₀= а sin πχ cos T, ω₀ = π, (1.34),

причем а=1 в (1.33).

Тогда первое приближение для продольного движения U₀

определяется из уравнения

, (1.35)

Где V₀ и ω₀ даются выражениями (1.34). Частное решение уравнения (1.35) имеет вид: , (1.36)

Подставляя V₀ и U₀ в выражение (1.26) для F₁ . получаем

, (1.37)

Теперь вывираем µ таким образом, чтобы функция Р₁ имела ту же величину, что и V₀ : , (1.38)

Затем определяем из (1.28) коэффициент һ₁ : һ₁=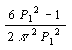,(1.39)

Первое приближение для основной частоты нелинейных колебаний имеет вид , (1.40)

Критическая скорость равна: , (1.41)

Или с учетом упрощений сделанных С.А. Панкратовым [2] формула (1.40) запишется в виде: , (1.42)

Тогда критическая скорость движения ленты равна , (1.43)

Без учета жесткости ленты частота поперечных колебаний и критическая скорость движения ленты определяется следующими соотношениями: , (1.44)

, (1.45)

Оценим влияние жесткости ленты, вычислив отношение

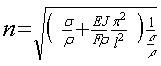
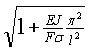= , (1.46)

Коэффициент n – характеризирующей влияние жесткости ленты на величину критической скорости движения, для обычных лент не превышает (1,05+1,1).

Второе приближение частоты нелинейных колебаний имеет вид:

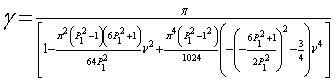, (1.47)

Тогда критическая скорость движения ленты равна

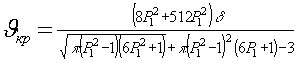, (1.48)

Более точные значения величины критической скорости движения ленты и частоты поперечных колебаний получим, используя уравнение колебаний ленты, полученное с учетом моментов инерций поворота сечений ленты и груза

, (1.49).

В первом приближений, используя то же метод, что и для упрощенного уравнения, можно получить:

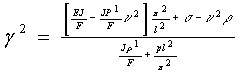, (1.50)

Значение критической скорости движения определяется по формуле: 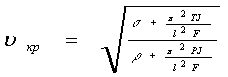, (1.51)

На рисунке показана зависимость частоты колебаний ленты от скорости ее движения.

----------- К=0, ________ К=1.0 -.-.-.-.-.-.- К=0.5

Литература

1. Гузь А.Н. Упругие волны в телах с начальными напряжениями – Киев.: Наукова Думка,1986.

2. Новожилов В.В. Основы нелинейной теории упругости.-М:ОГИЗ.1943.-212с.