Зелинская Т. В., Акишев Г.

Карагандинский Государственный Университет им. Е. А. Букетова, Караганда

Приближение суммируемых функций обобщенными средними Чезаро

Рассмотрим пространство всех - периодических измеримых по Лебегу функций для которых [1]

.

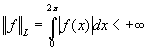Функцию разложим в ряд Фурье:

~,

где , - коэффициенты Фурье функции .

- частичная сумма ряда Фурье.

Для заданного числа величина

называется модулем гладкости -го порядка функции , где - конечная разность функции -го порядка с шагом , взятая в точке [1].

- наилучшее приближение функции тригонометрическими полиномами порядка не выше [1].

Для функции сопряженная функция определяется по формуле [2]:

.

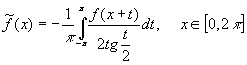Средняя Чезаро, или - средняя:

,

где .

При

,

называется средним арифметическим ряда Фурье или суммой Фейера.

Оценки величины через наилучшее приближение и модуль гладкости функции исследовали С.Б.Стечкин [3], П.Л. Ульянов, В.Э.Гейт [4], И.А.Буадзе [5] и другие.

В 1965 г. И.Б.Каплан [6] определил среднюю Чезаро с переменным порядком:

где - последовательность чисел ,.

В 2001 г. Т.Ахобадзе [7] доказал, что средние Чезаро с переменным порядком сходятся к .

Нами доказаны следующие утверждения:

Теорема 1. Пусть дана последовательность чисел . Тогда для любой функции справедливо неравенство:

.

Следствие 1. Пусть . Тогда для любой функции верно неравенство:

.

Следствие 2. Пусть . Тогда для любой функции справедливо:

.

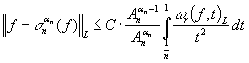Теорема 2. Пусть дана последовательность чисел , и

, (1)

тогда и

Замечание. В пространстве Лебега аналогичная задача рассмотрена в [8].

Литература:

1. Тиман А. Ф. Теория приближений функций действительного переменного. ГИФМЛ, М. 1960, – 624 с.

2. Бари Н. К. Тригонометрические ряды, ГИФМЛ, М. 1961,– 936 с.

3. Стечкин С.Б. О приближении периодических функций суммами Фейера. // Труды МИАН СССР, 1961. Т. 62. С.48-60.

4. Гейт В. Э. О точности некоторых неравенств в теории приближений // Матем. заметки. 1971, Т. 10, №5, С. 571–582.

5. Буадзе И.А. Об одной задаче П.Л.Ульянова, // Сообщ. Ан Груз. ССР, 1965, Т.40, №3, С.545-550

5. Каплан И. Б., О чезаровских средних переменного порядка, //Изв. вузов. Матем., 1960, - № 5, С. 62–73

6. Akhobadze T. On the convergence of generalized Cesaro means of trigonometric Fourier series. I //Acta Math Hungar., 2007, Vol. 115(1-2), P. 59-78.

7. Акишев Г.А., Суттибаева Г.Д. О приближении функций средними Чезаро с переменным показателем // Материалы девятой междунар. Казанской летней научной школы-конф. — Казань, 1–7 июля 2009. — С. 14–15.