Технічні науки / 3. Галузеве машинобудування

К.т.н. Гордєєв А.І., к.т.н. Урбанюк Є.А., к.т.н. Сілін Р.С.

Хмельницький національний університет

АНАЛІЗ ТА МОДЕЛЮВАННЯ ВІБРАЦІЙНИХ ТЕХНОЛОГІЙ З ВИКОРИСТАННЯМ ДВУХФАЗНИХ СЕРЕДОВИЩ ПРИ ВЗАЕМОДІЇ З ПОВЕРХНЕЮ, ЯКА ОБРОБЛЮЄТЬСЯ

У багатьох галузях промисловості усе більш широке застосування знаходять вібраційні технологічні процеси, у яких використовуються багатофазні середовища. Це можуть бути розплави металів, скла й полімерів, суспензії твердих часток і газових пухирців у рідині, дрібнодисперсні суспензії крапель у газоподібному чи рідкому середовищі тощо.

При здійсненні процесів, зв'язаних із необхідністю рівномірного розподілу різних фаз у рідкій основі (одержання композитів) або їхньої сепарації з рідини (дегазація і флотаційне збагачення), істотного значення набуває можливість прогнозування реакції таких систем на різного роду зовнішні періодичні впливи. Як показали раніше виконані дослідження динамічних явищ у багатофазних середовищах, підданих керованим вібраційним впливам, багато з них можуть бути успішно використані як для інтенсифікації зазначених процесів, так і при розробці та реалізації принципово нових технологічних прийомів, наприклад, знезараження води і зміни її властивостей.

Так, виникнення вібраційного переміщення включень у багатофазних середовищах сприяє більш ефективному їхньому очищенню від твердих і газоподібних домішок, організація періодичних режимів руху дрібнодисперсних фаз істотно спрощує процеси приготування однорідних суспензій і перемішування рідин.

Розглянемо ще один аспект руху багатофазного середовища – взаємодія його з поверхнею, оброблюється де включення газової або твердої фаз виконують роль інструменту, а рідина виступає як несуще середовище.

Оброблення матеріалів потоком твердих часток все більше поширюється в різних областях машинобудування.

Зокрема, це такі процеси: дробоструминне наклепування, струминно-абразивна обробка, пневмо-струминне очищення поверхонь від облою пластмасових армованих деталей кульками з полістиролу або абрикосовою дробленою кісткою, мийка поверхонь деталей пульсуючими струменями газорідинного потоку [1-3].

Головний практичний інтерес представляє встановлення виду залежностей між основними технологічними параметрами, такими, як розмір робочих тіл (кульок, абразивних зерен, газових пухирців) їхня швидкість руху, тиск робочого середовища, концентрація, кут атаки, фізико-механічні властивості часток і вихідні параметри процесу (шорсткість оброблюваної поверхні і величина наклепу поверхні та зняття матеріалу). Це обумовлено необхідністю оптимального вибору величин технологічних параметрів в умовах конкретного виду обробки поверхні.

Такі закономірності можуть бути встановлені в результаті регресивного аналізу експериментальних даних. Однак застосування отриманих залежностей обмежується порівняно вузькими межами зміни параметрів, довготривалими умовами проведення експериментів.

Більш універсальним є підхід, заснований на визначенні залежностей і вирішенні завдань оптимізації технологічних параметрів процесу обробки в результаті імітаційного моделювання. Такій підхід запропоновано автором [4,5] для струминно-абразивної обробки поверхонь. Реалізація такого підходу припускає побудову математичної моделі досліджуваного об'єкта.

Якщо ввести у математичну модель додаткові критерії та деякі аналітичні залежності, її можна застосовувати для аналізу більш широкого класу технологій, наприклад: мийки забруднень, гідродробозміцнення деталей, зняття облою з пластмасових деталей. Проведемо узагальнення даного підходу [4] для вище зазначених процесів.

Реальні технологічні особливості вищеозначених процесів, зокрема, дискретна природа потоку часток, указують на необхідність виконання послідовно

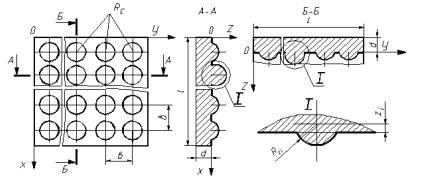
Рис. 1.1. Модель поверхні, яка підлягає обробленню [42]

одиничних актів конкретної взаємодії на елементарній ділянці оброблюваної поверхні. Мається на увазі досить мала квадратна площадка (рис. 1.1).

Отже, величина знімання матеріалу або забруднення може бути визначена як:

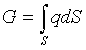, (1.1)

де S – площа оброблюваної поверхні, або яка очищується;

q – величина знімання матеріалу або забруднення з елементарної площадки. Тут:

,

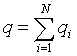де N – кількість одиничних актів контактної взаємодії на елементарній площадці;

– величина знімання матеріалу або забруднення після одиничного акта контактної взаємодії.

При цьому величина обумовлена технологічними параметрами процесу, шорсткістю поверхні і її властивостями. Разом із тим, зміна шорсткості поверхні в процесі обробки взаємопов’язана зі зміною величини знімання матеріалу або забруднення.

Таким чином, в основу математичної моделі процесу взаємодії потоку твердих або абразивних часток покладена модель одиничного акту контактної взаємодії, що дозволяє визначати величину .

Розглянемо рух двокомпонентного струменя з частками, які не взаємодіють між собою, а швидкість часток дорівнює швидкості потоку.

Показники фізико-механічних властивостей матеріалу часток (твердість, густина, коефіцієнт Пуассона, модуль пружності, міцність на зріз) є випадковими величинами з нормальним законом розподілу ймовірностей.

За встановленим радіусом частки і густині матеріалу розраховується маса частки, що рухається.

Величина кута атаки траєкторії частки залежить від технологічних особливостей процесу обробки, який моделюється. Наприклад, у випадку дослідження обробки потоком часток, сформованих соплом обладнання, можна допустити, що всі частки потоку мають однаковий кут атаки. При цьому величина кута може змінюватися в широких межах.

Кількість відтворених при моделюванні актів одиничної контактної взаємодії обумовлена концентрацією твердих часток у потоці, величиною витрат за одиницю часу через зріз сопла, співвідношенням величин площ сопла й елементарної площадки, часом і маршрутом переміщення оброблюваній поверхні відносно сопла.

Запропоновану авторами математичну модель [4,5] можна використовувати для визначення різних технологічних параметрів гідроструминної обробки: величини розмірів робочих часток, швидкості часток, величин кута атаки, величини сили контактної дії. Проводити аналіз процесу взаємодії газових пухирців із забрудненням при очищенні. Як критерій оптимізації для різних технологічних процесів природно приймати величину знімання матеріалу або площі забруднення в процесі мийки та очищення, або величину наклепу при дробоструминному обробленні. Величина шорсткості виступає як обмеження.

Тому задача оптимізації формулюється для запропонованих технологій у загальному вигляді:

;

(1.2)

;

,

де і – показники припустимої й досягнутої шорсткості поверхні;

– вага матеріалу, який знімається з поверхні або відповідно площа, яка очищена;

– діаметр насадка;

– сила удару по поверхні;

– кут атаки частки до поверхні;

V – швидкість.

Література:

1. Свиридов А. И. Исследование и расчет процесса очистки трубопроводов пульсирующим газожидкостным потоком / А. И. Свиридов, П. В. Балашов // Вестник машиностроения. – 1985. – № 11. – С. 33–35.

2. Гордєєв А. І. Дослідження процесу взаємодії пульсуючого газорідинного потоку з технологічними забрудненнями / А. І. Гордєєв // Вісник ТУП. Серія: Технічні науки. – 1997. – № 1. – С. 55–60.

3. А. с. 1297952 СССР, МКИ³ B 08 В 7/02. Устройство для очистки мелких изделий / А. И. Гордеев, М. А. Фетисов, С. А. Дытюк (СССР). – № 3978755/31–12 ; заявл. 22.11.85 ; опубл. 23.03.87, Бюл. № 11. – 3 с. : ил.

4. Имитационное моделирование процесса обработки потоком абразивных частиц / А. Э. Проволоцкий, А. Г. Ясев, В. С. Гришин, И. А. Маринченко // Изв. вузов. Машиностроение. – 1987. – № 4. – С. 112–116.

5. Проволоцкий А. Е. Струйно-абразивная обработка деталей машин / А. Е. Проволоцкий. – К. : Техника, 1989. – 177 с.