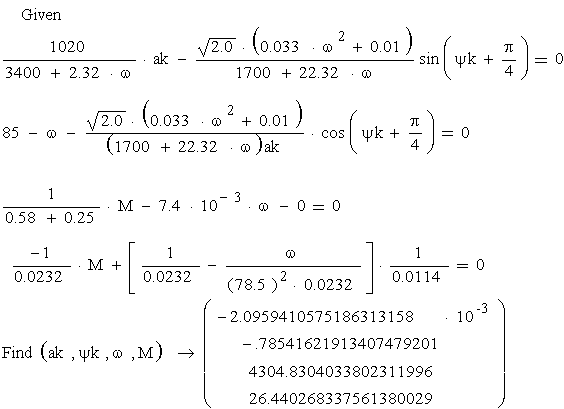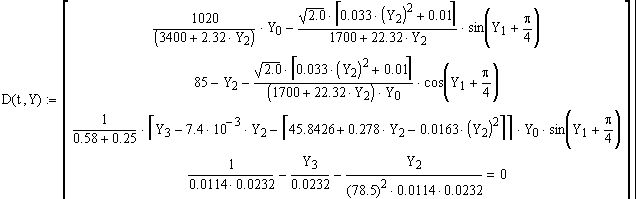К.т.н. Толубаева К.К.

 Восточно-Казахстанский государственный технический университет

 им. Д. Серикбаева, Казахстан

ДВИЖЕНИЯ ГИРОСКОПИЧЕСКОЙ РОТОРНОЙ СИСТЕМЫ С УЧЕТОМ ДИНАМИЧЕСКОЙ ХАРАКТЕРИСТИКИ ДВИГАТЕЛЯ

Уравнение движение гироскопической роторной системы с учетом динамических характеристик двигателя имеет вид:

 

     

                                                           (1)   

       

     

 

где  –  гироскопические члены уравнения

В данной постановке задачи момент двигателя зависит от времени t, т.к. четвертом уравнении производное от момента берется от времени t.

         Уравнение (1) являются нелинейным дифференциальным уравнениями с переменными коэффициентами, за счет связи с приводом.

При исследовании колебаний нелинейных гироскопических систем со многими степенями свободы построение асимптотических приближений в некоторых случаях можно привести так же, как для некоторой эквивалентной колебательной системы обладающей только одной степенью свободы. Исследования колебаний нелинейных систем был впервые предложен академиком Н.Н. Боголюбовым и позднее обобщен на нестационарные колебательные процессы Ю.А. Митропольским.

В колебательной системе по истечении некоторого времени должны установится колебания одного тона, что в большинстве случаев и происходит наличию диссипативных сил и внешних возмущений. Диссипативные силы обуславливают затуханию высших гармоник, и в системе устанавливаются колебания основного тона с частотой, близкой к частоте возмущающей силы.

Одночастотный метод позволяет рассмотреть как стационарные колебания роторов, так и процесс перехода ротора через критические числа оборотов при весьма общих условиях - с учетом гироскопического эффекта дисков и неодинаковой жесткости вала- обуславливающих переменных коэффициентов дифференциальных уравнений, при наличии упругих опор с нелинейной характеристической упругости и т.д.

    Единственным ограничением, определяющим возможность применения указанного метода, является требование медленного изменения угловой скорости по отношению к величине собственной частоты исследуемой системы, что практически выполняется даже для легких, быстроходных машин.

Увеличение числа степеней свободы не изменяет порядка системы уравнений первого и высших приближений, а приводит лишь к усложнению ее коэффициентов, что большинстве случаев несущественно увеличивает объем вычислительной работы при численном интегрировании этих уравнений.

Согласно асимптотическому одночастотному методу Боголюбова -Митропольского, решение первых 2-х уравнений системы  найдено в виде:

 

qj=acjei(l+y)+ac*je- i(l+y),                                                                            (2)

где q1=a, q2=b

         Амплитуда а и фаза y  рассмотрена как медленно меняющаяся функция времени и найдена из уравнений первого приближения:

        

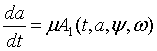
                                                                                  (3)

Для нахождения функций A1(t,a,y,w) и В1(t,a,y,w) использованы уравнения полученные Ю.А.Митропольским. Проведя соответствующие преобразования  получено:

 

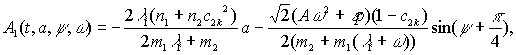
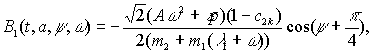                                      (4)

 

Амплитуда а и фаза y являются медленно изменяющимися функциями времени t, считая их для одного периода колебания постоянными, из уравнений найдены  Затем подставляя в правую часть 1-го уравнения системы  и усредняя их по φ за время, равное одному периоду, получено:

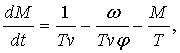                                                                            (5)

 

  Для решение системы необходимо найти начальные условия задачи.  Пологая Md0=Mn,

Применяя метод  Рунге - Кутта  систему решаем    использованием  программного обеспечения Mathcad. При численном решении задачи на ЭВМ были использованы следующие значения для роторной системы и двигателя.

 

                                      

        

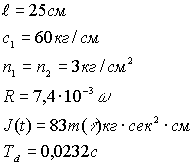
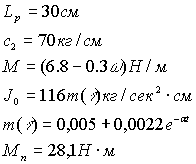
Текст программного    решения данной задачи: