Е.К.Щетинина

к.ф.-м.н., доцент кафедры высшей и прикладной математики

Донецкого национального университета экономики и торговли

имени М.Туган-Барановского

АСИМПТОТИЧЕСКИЕ ДВИЖЕНИЯ ГИРОСТАТА

К настоящему времени в динамике твердого тела с неподвижной точкой построено большое количество частных решений уравнений движения. Важным этапом в получении свойств движения тела (в более общем случае – гиростата) является исследование окрестности этих решений. Большой интерес в задаче изучения движения тела в окрестности известных решений представляют асимптотические движения. Эффективным методом анализа асимптотических решений служит первый метод Ляпунова.

В данной работе изучается задача о движении сферического гиростата под действием потенциальных и гироскопических сил, описываемая дифференциальными уравнениями Кирхгофа–Пуассона. С помощью первого метода Ляпунова изучаются условия существования асимптотических движений гиростата в случае, когда предельным движением является прецессия – регулярная, полурегулярная, общего вида. Рассматриваемые типы движений являются достаточно важными для приложений классов движения тела. Прецессии гиростата имеют наглядную механическую интерпретацию и находят широкое применение в теории гироскопических систем.

Следуя методике, предложенной Г.В.Горром и Д.И.Думбаем [1], в случае сферического гиростата найдено уравнение Хилла

(1)

для трех решений, полученных Г.В.Горром, А.В.Мазневым [2] и Н.В.Курганским [3].

В случае регулярной прецессии найдены две зоны неустойчивости:

,

,

для величин и из которых уравнение (1) допускает одно решение с положительным характеристичным числом. Это соответствует асимптотически прецессионным движениям гиростата, для которых регулярная прецессия является предельным движением.

Для случая полурегулярной прецессии второго типа найдена первая зона неустойчивости решения уравнения (1)

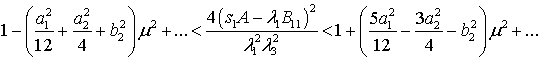, что позволило установить новые решения уравнений Кирхгофа–Пуассона в виде однопараметрических рядов Ляпунова, описывающих движения гиростата, которые при стремятся к полурегулярной прецессии второго типа относительно вертикали. Это означает, что при определенном выборе начальных данных движение гиростата при будет стремиться к полурегулярной прецессии второго типа. Аналогично можно найти и другие условия существования положительного характеристичного числа уравнения (1). Важно, что эти условия связаны с тем, что зоны неустойчивости (или существования асимптотически прецессионных движений) имеют место в окрестности значения (где – натуральное число).

В случае прецессионного движения общего вида уравнение Хилла (1) преобразуется к виду

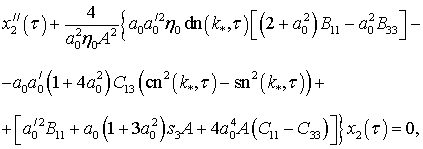(2)

где штрихом обозначено дифференцирование по обобщенному времени .

Вид уравнения (2) позволяет указать достаточные условия существования у него решений с положительным характеристичным числом. Для этого применено достаточное условие Ляпунова [5]: , где – коэффициент при в уравнении (2). Представим свободный член функции в виде

(3)

Предположим, что в (2), (3) параметр и принимает большие по абсолютной величине значения. Тогда в силу ограниченности эллиптических функций можно добиться условия для любых значений , что означает существование одного решения уравнения (2) с положительным характеристичным числом. Тем самым показано существование асимптотических движений гиростата, предельное движение которых описывается прецессией общего вида.

Таким образом, на основании первого метода А.М.Ляпунова установлены новые решения уравнений Кирхгофа–Пуассона в виде рядов Ляпунова, описывающих движения сферического гиростата, которые при стремятся к прецессии относительно вертикали. Все установленные в работе движения описываются однопараметрическими рядами Ляпунова.

1. Горр Г.В., Думбай Д.И. Об асимптотически прецессионных движениях гиростата в обобщенной задаче динамики // Механика твердого тела. – 1994. – Вып. 26 (I). – С. 20-28.

2.Горр Г.В., Мазнев А.В., Верховод Е.В. Новые решения обобщенной задачи динамики твердого тела с неподвижной точкой // Докл. АН Украины. Сер. А. Физ.–мат. и техн. науки. – 1992. – № 5. – С. 50-54.

3. Курганский Н.В. О полурегулярной прецессии первого типа относительно вертикали в одной задаче динамики твердого тела // Механика твердого тела. – 1988. – Вып. 20. – С. 67-71.

4. Малкин И.Г. Теория устойчивости движения. – М.: Наука, 1968. – 530 с.