О.С.Сатыбалдиев

Казахский национальный технический университет им. К.И.Сатпаева, Республика Казахстан

 

Критерий конечности типа одного несамосопряженного дифференциального оператора типа Шредингера

 

Пусть -замыкание в  дифференциального оператора определенного на  равенством

где -оператор Лапласа, -положительное целое число, -ограниченная в каждом компакте комплекснозначная функция, такая, что

                                                                                                       (1)

Введем некоторые необходимые обозначения и определения.

-емкость замкнутого множества  относительно открытого множества , содержащего  , называется число

где

  берется во всем , равным единице в окрестности . Через  куб с центром в точке ,  с ребрами, равными , параллельным координатами осями, а через -его замыкание. Если положение центра куба не важно, вместо  и  будем писать  и  соответственно. Совокупность всех компактных подмножеств  куба , удовлетворяющих неравенству

                                                                                 (2)

обозначим через  При  и достаточно малом  множество  пусто. Этот факт следует из непрерывности оператора вложения пространства  в пространство непрерывных функций.

Теперь ограниченной в каждом компакте комплекснозначной функции   сопоставим функцию

                                                                      (3)

При функция  не зависит от  и определяется формулой

                                                                   (4)

 

                                                   (5)

Пусть далее  обозначает количество -чисел оператора  не превосходящих .

Теорема1 [2, стр.35]. Пусть -функция, определенная одной из формул (3) и (4). Предположим, что выполнены следующие условия:

а)                                                          (6)

где -непрерывная функция, стремящаяся к  при (2) при  

б) при некотором

                                                                                                 (7)

в) оператор  вполне непрерывен.

Тогда для любого  справедливы оценки

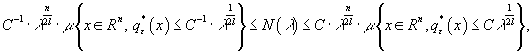                   (8)

где -мера Лебега, -постоянная, зависящая только от постоянной  из условия (6).

Основная теорема. Пусть  и выполнены условия а)-в) теоремы 1. Тогда:

 резольвента оператора  принадлежит классу  в том и только в том случае, если

                                           ;                                                      (9)

 справедливы оценки

                                                          (10)

Доказательство. Достаточность. Пусть выполняется условие (9). По определению имеем

Теперь воспользуемся правой из неравенств (8). Тогда получим

Отсюда вытекает справедливость правой из неравенств (10) и утверждения (9) в достаточную сторону.

Необходимость. Пусть оператор  т.е.

где -числа оператора . Тогда левой из неравенство (8) получим

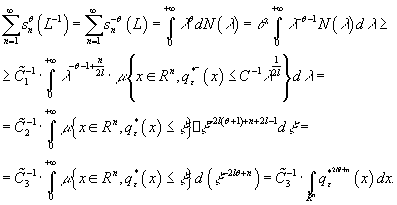
Отсюда вытекает справедливость левой из неравенств (10) и утверждения (9) в необходимую сторону.

Основная теорема  полностью доказана.

 

Литература

1.     Отелбаев М., Оценка спектра эллиптических операторов и связанные с ними теоремы вложения, Докт..., дисс.,  М., МГУ, 1978.

2.     Сатыбалдиев О.Об оценках -чисел и полноте системы корневых векторов некоторых дифференциальных операторов, Канд…, дисс., Алматы, 1988.