Экономические науки/8 математические методы в экономике

Дмитренко Ирина Сергеевна

к.ф-м.н. Колесников Сергей Алексеевич

Донбасская государственная машиностроительная академия

Кафедра высшей математики

Применение методов классической оптимизации и функциональных уравнений Беллмана при решении задач о распределении инвестиций.

Среди экономически важных задач большой интерес представляет проблема распределения капитальных вложений между отраслями или предприятиями отрасли. Постановка таких задач, а значит и подбор соответствующего метода решения, зависит от способа задания функции дохода предприятия. В данной работе рассмотрены два способа задания функции доходности и предложены следующие методы решения : 1) метод классической оптимизации, предусматривающий исследование непрерывной функции многих переменных на экстремум с помощью построения функции Лагранжа, 2) метод обратной прогонки динамического программирования для дискретной функции дохода, предусматривающий составление функциональных уравнений Беллмана.

Рассмотрим вначале метод динамического программирования для решения следующей задачи. Совет директоров фирмы рассматривает предложения относительно прироста производственных мощностей для увеличения выпуска однородной продукции на четырех предприятиях, принадлежащих фирме. Для модернизации предприятий предложено инвестировать средства в объеме 250 усл.ден.ед. с дискретностью 50 усл.ден.ед. Прирост выпуска продукции зависит от выделенной суммы ,а его значения даны предприятиями и содержатся в таблице. Найти распределение инвестиций между предприятиями, обеспечивающее фирме максимальный прирост продукции, при чем на одно предприятие можно осуществить только одну инвестицию.

Инвестиции, усл.ден.ед.	Прирост выпуска продукции, усл.ден.ед.
	g1(x)	g2(x)	g3(x)	g4(x)
50	8	10	12	11
100	16	20	21	23
150	25	28	27	30
200	36	40	38	37
250	44	48	50	51

Запишем уравнение Беллмана для метода обратной прогонки и разобьем решение задачи на 4 этапа.

Этап 4. F₅(C₅)=0

C4	F4(C4)=g4(x4)						оптимум
	X4=0	X4=50	X4=100	X4=150	X4=200	X4=250	F4(C4)	X4^*
0	0	-	-	-	-	-	0	0
50	-	11	-	-	-	-	11	50
100	-	-	23	-	-	-	23	100
150	-	-	-	30	-	-	30	150
200	-	-	-	-	37	-	37	200
250	-	-	-	-	-	51	51	250

Этап 3.

C3	F3(C3)=g3(x3)+ F4(C3-x3)						оптимум
	X3=0	X3=50	X3=100	X3=150	X3=200	X3=250	F3(C3)	X3^*
0	0+0=0	-	-	-	-	-	0	0
50	0+11=11	12+0=12	-	-	-	-	12	50
100	0+23=23	12+11=23	21+0=21	-	-	-	23	0,50
150	0+30=30	12+23=35	21+11=33	27+0=27	-	-	35	50
200	0+37=37	12+30=42	21+23=44	27+11=38	38+0=38	-	44	100
250	0+51=51	12+37=49	21+30=51	27+23=50	38+11=49	50+0=50	51	0,100

Этап 2.

C2	F2(C2)=g2(x2)+ F3(C2-x2)						оптимум
	X2=0	X2=50	X2=100	X2=150	X2=200	X2=250	F2(C2)	X2^*
0	0+0=0	-	-	-	-	-	0	0
50	0+12=12	10+0=10	-	-	-	-	12	0
100	0+23=23	10+12=22	20+0=20	-	-	-	23	0
150	0+35=35	10+23=33	20+12=32	28+0=28	-	-	35	0
200	0+44=44	10+35=45	20+23=43	28+12=40	40+0=40	-	45	50
250	0+51=51	10+44=54	20+35=55	28+23=51	40+12=52	48+0=48	55	100

Этап 1.

C1	F1(C1)=g1(x1)+ F2(C1-x1)						оптимум
	X1=0	X1=50	X1=100	X1=150	X1=200	X1=250	F1(C1)	X1^*
0	0+0=0	-	-	-	-	-	0	0
50	0+12=12	8+0=8	-	-	-	-	12	0
100	0+23=23	8+12=20	16+0=16	-	-	-	23	0
150	0+35=35	8+23=31	16+12=28	25+0=25	-	-	35	0
200	0+45=45	8+35=43	16+23=39	25+12=37	36+0=36	-	45	0
250	0+55=55	8+45=53	16+35=51	25+23=48	36+12=48	44+0=44	55	0

Из таблицы этапа 1 находим оптимальное значение целевой функции при распределении между предприятиями всей суммы С₁=250: F₁(250)=55. При этом первому предприятию должно быть выделено x₁^*=0 ден.ед. Тогда остальным трем предприятиям остается распределить С₂=С₁-x₁^*=250-0=250 ден.ед. Из таблицы этапа 2 выделению суммы С₂=250 соответствует значение x₂^*=100, тогда С₃=С₂- x₂^*=250-100=150 ден.ед. Из таблицы этапа 3 выделению суммы С₃=150 соответствует значение x₃^*=50, тогда С₄=С₃- x₃^*=150-50=100 ден.ед. На последнем этапе 4 определяем x₄^*=100.

Таким образом, оптимальный план инвестирования предприятий:

X^*= (0,100,50,100), который обеспечит максимальный доход, равный

F(250)=g₁(0)+g₂(100)+g₃(50)+g₄(100)=0+20+12+23=55 усл.ден.ед.

Вторая задача имеет похожую постановку, но функции дохода являются нелинейными. Для модернизации трех предприятий совет директоров инвестирует средства в объеме 150 денежных единиц. Пусть приросты выпуска продукции, а значит и общего дохода, зависят от выделенной суммы для i-го предприятия и выражаются соответствующими квадратичными зависимостями:

Найдем методом множителей Лагранжа распределение инвестиций между предприятиями, которое обеспечит фирме максимальный прирост продукции.

Перед тем, как составить функцию Лагранжа, запишем функцию суммарного дохода предприятий:

Тогда функция Лагранжа имеет вид:

Точку условного экстремума определим из необходимого условия экстремума функции многих переменных:

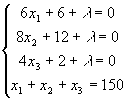
Таким образом, координаты искомой точки экстремума имеют вид: .

Отметим, что решение аналогичных практических задач данными методами является наглядной иллюстрацией методов оптимизации непрерывных и дискретных функций дохода предприятия. Отметим также, что данные примеры позволят будущим специалистам в дальнейшем правильно анализировать экономико-математические производственные модели и подбирать соответствующий эффективный метод для их решения.

Литература

1. Ляшенко И.Н., Карагодова Е.А., Черникова Н.В., Шор Н.З. Линейное и нелинейное программирование. Киев, «Высшая школа», 1975. 350-351с.

2. Таха, Хэмди А. Введение в исследование операций. -М.:Изд.дом «Вильямс», 2001.-447-452с.