Магистрант 2-го года
Исабеков С., к.т.н., доцент
Балабеков Б.Ч.
ЮКГУ имени М.О. Aуeзoвa, г. Шымкент
МАТЕМАТИЧЕСКИЕ АСПЕКТЫ
ПРЕОБРАЗОВАНИЙ, ИСПОЛЬЗУЕМЫХ В КОМПЬЮТЕРНОЙ ГРАФИКЕ
Компьютерная графика глубоко проникла в самые разные области жизни
современного общества /1-3/. Среди главных сфер применения компьютерной графики
выделяют следующие: визуализация информации, техническое черчение,
моделирование с элементами мультипликации, создание интерфейса пользователя.
Графический образ как способ передачи информации намного эффективней любого
другого способа. Компьютерная графика применяется для вывода как двумерных, так
и трехмерных графиков различных зависимостей, статистических гистограмм, полигонов,
диаграмм, полученных из экономических данных. В современных системах
автоматизированного проектирования компьютерная графика используется для
проектирования узлов и частей технических электрических, механических и
электронных систем. Например, корпус лайнера, информационные сети,
энергетические установки. При этом основное внимание уделяется установлению
взаимодействия оператора с проектируемой деталью. С помощью компьютерной
графики появилась возможность увидеть на экране движение жидкости в канале,
протекание химической и ядерной реакции, образование трещин конструкции под
нагрузкой. Также появились различные симуляторы, которые моделируют реальную
действительность, такие системы сначала освоили пилоты при подготовке в тренажерных
залах. Примерами пользовательского интерфейса являются графическая оболочка
операционных систем. В нее входят различного рода пиктограммы, кнопки, меню,
ярлыки, которые можно легко активизировать с использованием "мыши".
Надо упомянуть также о графических программах – броузерах, которые облегчают
работу миллионам людей в сети Интернет.
Перед выводом на экран любое изображение претерпевает целый
ряд разнообразных преобразований: повороты, переносы, отображения, масштабирования
и их композиции. В настоящей работе рассматриваются математические аспекты
отображений. Рассмотрим отображение относительно плоскости в пространстве.
Общее уравнение плоскости имеет вид
ax+by+cz+d=0 (1)
его можно привести к виду
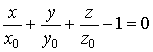 (2)
(2)
Для простоты дальнейшего
изложения наложим следующее условие:
![]() (3)
(3)
Тогда плоскость (2) в первом
октанте можно изобразить как на рисунке 1. Плоскость (2) пересекается с
координатной плоскостью «xy» как показано на
рисунке 2.
На рисунке 2 приведены линия
«l», перпендикулярная отрезку «x0y0» и линия «k» параллельная
оси «x». Также показаны угол a и высота «h» в
треугольнике «0x0y0». Для определения «a» и «h» можно записать следующие
выражения:
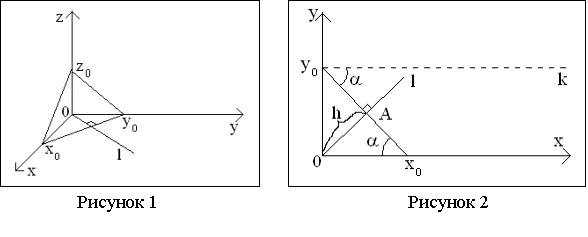
tga = ![]() , h = x0sina (4)
, h = x0sina (4)
Точка (А) на рисунке 2 имеет
следующие координаты
(hsina, hcosa) (5)
На рисунке 3 показана
плоскость «zl», где линия «l» лежит в плоскости «xy» (см.
рисунок 2). Из рисунка 3 определяем угол b:
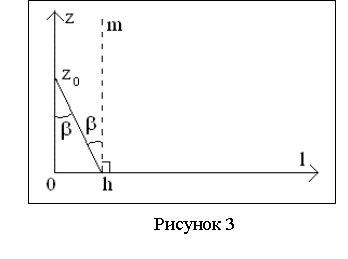
tgb = ![]() , (6)
, (6)
Теперь можно написать
композицию простых преобразований для выполнения отображения относительно
плоскости (2):
- параллельный перенос
плоскости (2) в начало координат, используя точку (А) из (5);
- поворот на угол (a) вокруг оси «z», чтобы отрезок x0y0
стал параллелен оси «x» (линия «k» на рисунке
2);
- поворот на угол (- b) вокруг оси «x», чтобы плоскость (2) стала
параллельна плоскости «xz» (линия «m» на
рисунке 3);
- отображение относительно плоскости «xz»;
- обратный поворот на угол (b);
- обратный поворот на угол
(- a);
- параллельный перенос
плоскости (2) в исходное положение.
Матричное представление этой
композиции имеет следующий вид в однородных координатах:
 (7)
(7)
Таким образом, получено
матричное выражение для отображения относительно произвольной плоскости в
пространственном случае. Подобные соотношения могут быть использованы при
создании графических систем различного назначения, а также могут быть заложены
в микропрограммы при изготовлении специализированных графических процессоров.
Литература
1. Роджерс Д., Адамс Дж.
Математические основы машинной графики. Пер. с англ. – М.: Машиностроение,
1980. – 240 с.: ил.
2. Эйнджел Э. Интерактивная
компьютерная графика. Вводный курс на базе OpenGL, 2 изд.: пер.с англ. – М.:
Издательский дом “Вильямс”, 2001. – 592 с.: ил.
3. Роджерс Д.
Алгоритмические основы машинной графики Пер. с англ. – М.: Мир, 1989. – 512 с.
ил.