Современные информационные технологии / Компьютерная
инженерия
Пардаев А.С.
УО «Белорусский государственный технологический университет»,
Беларусь
Моделирование
формы поперечного сечения
пиломатериалов из древесины при усушке
Введение. Многие задачи, с которыми сталкиваются исследователи и
инженеры при разработке рациональных режимов сушки пиломатериалов и заготовок
из древесины, не поддаются аналитическому решению либо требуют значительных
затрат времени на выполнение расчетов, создание опытных образцов и проведение
экспериментальных работ. Изучение объектов разработки путем проведения
экспериментов на их математических моделях, реализованных на ЭВМ, является
средством быстрого, а иногда и единственно возможного решения инженерных задач.
Одной из важных задач
древесиноведения является изучение деформативности древесины. Влажностные
напряжения, возникающие в древесине при усушке и разбухании, являются одним из
главных факторов, ограничивающих эксплуатацию конструкций и изделий из
древесины в среде с переменной влажностью. В таких условиях древесина меняет
форму и размеры, что может приводить к снижению качества изделий из древесины.
Поэтому становится актуальной разработка математических моделей и методик
оценки коробления пиломатериалов и заготовок из древесины при усушке, которые
могут быть реализованы с применением ЭВМ для последующего расчета их деформаций.
Целью данной работы
является разработка математической модели деформаций пиломатериалов и заготовок
из древесины, возникающих при усушке, и последующая ее реализация на ЭВМ, что позволило
производить расчет формы поперечного сечения покоробленных досок в
автоматическом режиме.
Основная
часть. При разработке модели
деформаций пиломатериалов и заготовок из
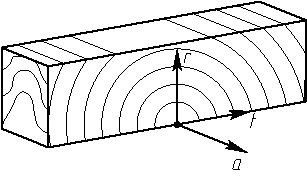
древесины принята криволинейная расчетная схема физико-механической
анизотропии древесины на основе цилиндрической системы координат [1], которая
позволила учесть структурные особенности этого материала при рассмотрении
процесса усушки.
Математическое описание модели деформаций пиломатериалов и заготовок из древесины [2]
проведено на основе теории упругости и метода конечных элементов. В процессе
моделирования осуществляется замена пиломатериалов
и заготовок из древесины на дискретную математическую модель, представляющую
собой совокупность элементарных объемов заданной формы (конечных элементов),
которые связанны между собой в граничных точках. Нагрузки и воздействия
(механические, влажностные), условия закрепления модели пиломатериалов и заготовок из древесины, а также расчет их
деформаций в узлах конечных элементов производятся в соответствии с общими
положениями метода конечных элементов.
Проверку разработанной модели деформаций пиломатериалов и заготовок из древесины
проводили путем сопоставления результатов расчета деформированного состояния доски
из древесины сосны с результатами, полученными в ходе эксперимента, а также соответствующими
известными аналитическими решениями [3].
|
|
|
Рисунок 1 – Трехмерная модель |
Исследовали поперечную покоробленность доски,
на нижней пласти которой находится сердцевина (рисунок 1). Сравнивали максимальную
стрелу прогиба образца в поперечном сечении при его усушке полученную в
результате эксперимента, моделирования деформированного состояния и аналитического
решения.
На рисунке 2 изображен внешний вид образцов
после окончания эксперимента. Средняя конечная влажность равна 7,1% и 7,0% для
образцов сечением 38´140 мм и 24´140 мм соответственно. Максимальная стрела прогиба,
как выборочное среднее экспериментальных данных, равна 3,25 мм и 3,33 мм для
образцов сечением 38´140 мм и 24´140 мм соответственно.
|
|
|
|
а) |
б) |
|
а
– образец сечением 38´140 мм;
б – образец сечением 24´140 мм |
|
|
Рисунок 2 – Внешний вид образцов после окончания
эксперимента |
|
Из результатов статистической обработки
данных следует, что конечная влажность образцов после их сушки характеризуется
высоким коэффициентом вариации – до 17%. Это означает что деформации, в
процессе сушки образцов, возникают не только вследствие анизотропии усушки древесины,
но и имеющегося градиента влажности. Данный факт, оказал влияние на величину
деформаций образцов при их усушке и потребовал подготовки индивидуальных моделей
по каждому образцу с учетом неравномерного распределения влажности по его
сечению.
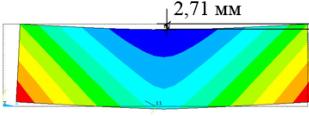
На рисунке 3 показан
результат моделирования деформаций образцов
сечением 38´140 мм и сечением 24´140 мм с учетом неравномерного распределения
конечной влажности по их сечению. Максимальная стрела прогиба при моделировании
деформированного состояния указанных образцов равна 2,71 мм и 2,86 мм
соответственно. Выбор образцов обусловлен наиболее равномерным распределением
влажности по их сечению, что позволяет с большей степенью точности подготовить
модели образцов. Для указанных образцов максимальная стрела прогиба, в
соответствии с экспериментальными данными, равна 3,01 мм и 3,11 мм, что с
погрешностью не более 10% соответствует результатам моделирования.
Отклонение экспериментальных данных от
результатов моделирования можно объяснить тем, что в процессе моделирования
физико-механические свойства древесины для всех образцов приняты одинаковыми,
однако в соответствии с ГСССД 69-84 различия в свойствах древесины может
колебаться в пределах 5–10%, а средний коэффициент вариации модулей упругости,
принятых в качестве исходных данных, составляет 20%, что, несомненно, вносит погрешность
в результаты расчета.
|
-2,71мм -0,51 мм 2,09 (мм) |
-2,86мм -1,25 мм 1,35 (мм) |
|
а) |
б) |
|
а
– образец №2 сечением 38´140 мм; б – образец №9
сечением 24´140 мм |
|
|
Рисунок 3 – Результат моделирования образцов:
исходная и |
|
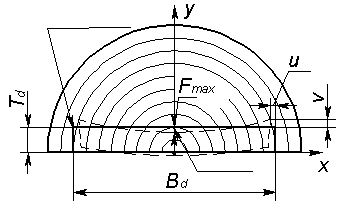
Аналитически форма поперечного сечения
покоробленных образцов определена по следующим известным уравнениям [3]:
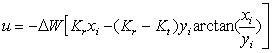
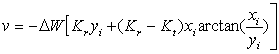
где 
и 
величина перемещения точек 1 и 2 поперечного сечения образца после
высыхания (рисунок 4);
и 
координаты точек 1 и 2 до высыхания;
– перепад
влажности между пределом насыщения
клеточных стенок 
и конечной
влажностью древесины 
;
, 
– коэффициент усушки
в радиальном и тангенциальном
направлении
соответственно (для сосны 
=0,002498 и 
=0,001527).
|
|
|
Рисунок 4 – Схема поперечной покоробленности
образца, |
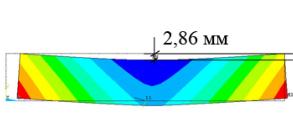
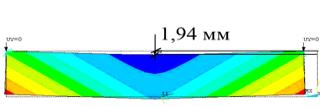
В результате аналитического решения
поставленной задачи максимальная стрела прогиба равна 1,67 мм и 1,94 мм для
образцов сечением 38´140 мм и 24´140 мм соответственно, что с погрешностью не более 1 %
соответствует результатам моделирования деформированного состояния образцов при
тех же условиях (1,68 мм и 1,94 мм соответственно рисунок 5).
|
-1,68мм 0,43 мм 2,12 (мм) |
-1,94мм -0,48 мм
1,36 (мм) |
|
а) |
б) |
|
а – образец сечением 38´140 мм; б
– образец сечением 24´140 мм |
|
|
Рисунок 5 – Результат
моделирования образцов по усредненным |
|
Заключение. Разработанная математическая модель деформаций элементов
конструкций из древесины по усредненным показателям с погрешностью не более 1%
соответствует известным аналитическим решениям и с погрешностью не более 10%
соответствует аналогичным экспериментальным данным по реальному объекту с
учетом изменения его влажности по сечению. Поскольку средние коэффициенты
вариации исходных данных для моделирования элемента конструкции из древесины
при усушке колеблются в пределах 10–28% то в соответствии с рекомендациями [3]
можно констатировать удовлетворительное согласие результатов расчета и эксперимента.
Следовательно, принятая схема анизотропии древесины и предложенная модель деформаций пиломатериалов и заготовок из
древесины адекватно отражает процесс изменения их формы и размеров при
усушке.
На основе предложенной модели деформаций пиломатериалов и заготовок из
древесины разработана программа на языке APDL [4] по расчету формы пиломатериалов
и заготовок при усушке. Она позволяет создать параметрическую трехмерную модель
пиломатериалов и заготовок и
автоматически произвести расчет их деформированного состояния.
Литература:
1.
Пардаев,
А.С. Моделирование физико-механических свойств древесины при конечно-элементном
анализе столярных изделий / А.С. Пардаев // Деревообработка: технологии,
оборудование, менеджмент XXI века: труды III Междунар. евразийского симпозиума,
Екатеринбург, 30 сентября 2008 г./ УГТУ; научн. редактор: В.Г. Новоселов –
Екатеринбург, 2008. – С. 77–83.
2.
Пардаев, А.С.,
Обеспечение формоустойчивости неоднородных массивов древесины с учетом
цилиндрической анизотропии их элементов при усушке и разбухании: автореф. дис.
... кан. техн. наук: 05.21.05 / А.С. Пардаев; БГТУ. – Минск, 2008. – 21 с.
3.
Уголев, Б. Н.
Древесиноведение с основами лесного товароведения: Учебник для лесотехнических
вузов / Б. Н. Уголев. – 5-е изд. – Москва: МГУЛ, 2007. – 340 с.
4.
Kent, L. Lawrence ANSYS Tutorial Releases 10
/ Kent L. Lawrence – University of Texas at Arlington: SDC Publications. – 2006