Сафонов А.А.
Национальный ядерный исследовательский университет
Новоуральский государственный технологический институт, Россия
Оптимизированный под машинную реализацию алгоритм «Крайних множеств» для построения выпуклой оболочки для множества точек плоскости.
Построение выпуклой оболочки – одна из фундаментальных задач вычислительной геометрии. Определение выпуклой оболочки для n-мерного пространства было дано ещё в 1966 году, и с тех пор предложены различные варианты решений этой задачи, самые известные и широко используемые из которых метод обхода Грэхема (1972), обход методом Джарвиса (1973), метод разделяй и властвуй (1974) [1,2].
Все обозначенные алгоритмы поддаются машинной реализации, однако изначально не могли учитывать её особенности и их эффективность значительно падает с увеличением количества точек. Автором разработан новый алгоритм построения выпуклой оболочки для множества точек плоскости, в котором используются специфические преимущества реализации алгоритма на машинных языках, благодаря чему достигается более высокая эффективность его применения для обсчёта множеств, характеризующихся высокими мощностями – алгоритм крайних множеств.
Постановка задачи. Пусть на плоскости задано множество n точек, определяющихся массивами декартовых координат. Необходимо найти точки, принадлежащие выпуклой оболочке для данного множества точек.
Шаг 1. Массив с координатами точек сортируется по оси абсцисс и ординат рекуррентным методом быстрой сортировки [2].
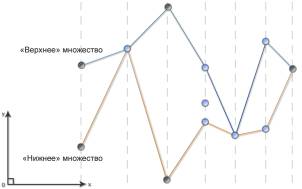
Шаг 2. После сортировки известны координаты крайних по оси абсцисс точек (точки с наименьшей и наибольшей абсциссой). Сортировка по оси ординат обеспечивает определение наивысшей и наинизшей точек при заданном значении x. При передвижении слева направо по абсциссам заданных точек определяются наивысшая и наинизшая точки, образующие два множества: «верхнее» и «нижнее». Если при очередном значении x имеется только одна точка, она считается принадлежащей обоим множествам. Таким образом, полученные множества будут упорядоченными по значениям абсцисс (рис. 1).
Рис. 1. Выделение верхнего и нижнего подмножеств. |
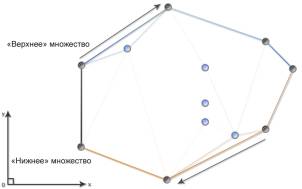
Рис. 2. Удаление лишних точек из подмножеств. |
|
|
|
|
Рис. 3. Устранение заломов, искомая выпуклая оболочка. |
|
Шаг 3. Действия над «верхним» и «нижним» множествами идентичны, поэтому рассмотрим операции над «верхним» множеством. При перемещении по оси абсцисс от первой точки массива до наивысшей отбрасываются точки, ордината которых меньше ординаты предыдущей точки (выполняются простейшие операции сравнения). Аналогично производится перемещение от последней точки до наивысшей (рис. 2). Иногда этих операций уже достаточно для получения контура выпуклого многоугольника.
Шаг 4. Ликвидация «заломов». Проверяется, находится ли средняя точка из трёх подряд идущих точек «выше» прямой, образованной двумя другими точками (для «нижнего» множества – «ниже»): на данной прямой находится точка с абсциссой, равной абсциссе средней точки; если её ордината меньше (для «нижнего» множества – больше) ординаты средней точки, то точка исключается. Таким образом, получаем верхнюю и нижнюю части выпуклого многоугольника (рис. 3). Осталось их соединить.
Последний шаг можно было применить сразу после второго, но на четвёртом шаге происходит больший расход процессорного времени (операция расчёта координаты точки, лежащей на прямой, и операция сравнения), чем на третьем шаге (только операция сравнения). Поэтому «быстрый» отсев точек на третьем шаге значительно ускоряет заключительную проверку на выпуклость.
Для определения эффективности алгоритма было проведено сравнительное исследование, позволяющее определить трудоёмкость его работы на множествах различной мощности и сравнить с известными. На языке Delphi в среде программирования Borland® Delphi 7 были написаны программы, выявляющие расход времени на построение выпуклой оболочки следующими алгоритмами: обход методом Джарвиса, метод обхода Грэхема, разделяй и властвуй и алгоритм крайних множеств автора. Максимальная мощность множества ограничивается 10000 точками. Начальное значение – 10 точек.
Для каждой мощности множества точек было проведено не менее 100 запусков процедуры построения выпуклой оболочки каждым из алгоритмов для различной комбинации входных данных. За результат работы алгоритма на данной мощности множества бралось среднее арифметическое значение временного интервала. Расчёты проводились на ПК с конфигурацией Intel® Pentium® IV CPU 2 GHz/512 Mb. Результаты работы алгоритмов представлены таблично (табл. 1) и графически (рис. 4).
Из рис. 4 видно, что на малых множествах самым быстрым методом построения
выпуклой оболочки оказался алгоритм Грэхема.
На множествах мощностью 225 точек его обгоняет алгоритм крайних множеств, и уже на множествах мощностью в 415
точек оказывается самым быстрым
алгоритмом, стабильно сохраняя преимущественную эффективность на множествах с
более высокими мощностями.
Таблица 1. Временные
характеристики алгоритмов
|
количество
точек (шт) |
Алгоритм
Джарвиса (мс) |
Алгоритм |
Алгоритм |
Алгоритм
крайних |
|
10 |
0,033 |
0,036 |
0,134 |
0,073 |
|
15 |
0,055 |
0,039 |
0,162 |
0,075 |
|
20 |
0,079 |
0,041 |
0,183 |
0,078 |
|
30 |
0,134 |
0,046 |
0,218 |
0,084 |
|
45 |
0,222 |
0,055 |
0,259 |
0,092 |
|
70 |
0,383 |
0,068 |
0,314 |
0,104 |
|
105 |
0,627 |
0,090 |
0,377 |
0,117 |
|
160 |
1,037 |
0,121 |
0,462 |
0,137 |
|
240 |
1,693 |
0,169 |
0,576 |
0,164 |
|
360 |
2,729 |
0,239 |
0,728 |
0,203 |
|
540 |
4,389 |
0,349 |
0,943 |
0,260 |
|
810 |
7,029 |
0,512 |
1,238 |
0,345 |
|
1215 |
11,140 |
0,762 |
1,648 |
0,478 |
|
1820 |
17,634 |
1,140 |
2,208 |
0,693 |
|
2730 |
27,258 |
1,718 |
2,916 |
1,032 |
|
4095 |
42,817 |
2,602 |
3,864 |
1,546 |
|
6140 |
65,240 |
3,934 |
4,985 |
2,340 |
|
9210 |
99,782 |
5,968 |
6,188 |
3,578 |
|
10000 |
106,410 |
6,534 |
6,725 |
3,846 |
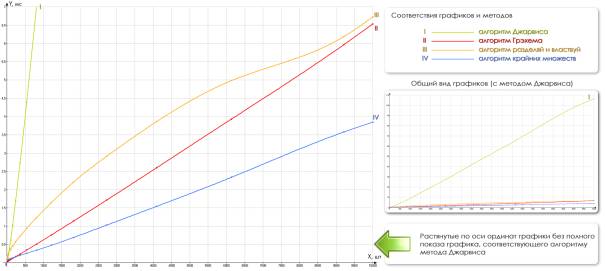
Рис. 4. Графики временных
характеристик алгоритмов.
Предложенный алгоритм крайних множеств использует максимум возможностей сортировки элементов и простейших машинных операций, обеспечивая высокое быстродействие на множествах с большим количеством точек. В результате получается не только уже упорядоченный набор элементов решения как такового (что повышает скорость построения соответствующей визуализации или любого другого практического применения), но и полученный промежуточный результат из двух «верхнего» и «нижнего» множеств позволит оптимизировать время решения задач, основа которых подразумевает предварительное построение выпуклой оболочки.
Литература
1. Препарата Ф., Шеймос М. Вычислительная геометрия: Введение: Пер. с англ. // М.:Мир, 1989. – 478 с.
2. Ласло М. Вычислительная геометрия и компьютерная графика на C++: Пер. с англ. // М.: БИНОМ, 1997. – 304 с.