Проблемы
подготовки специалистов
З.А.Маханова
ЮКГУ им.М.О.Ауезова, г.Шымкент, Республика Казахстан
ВОЗМОЖНОСТИ
ОБУЧЕНИЕ МАТЕМАТИКЕ СТУДЕНТОВ СПЕЦИАЛЬНОСТИ
«ИНФОРМАЦИОННЫХ СИСТЕМ» ПО
ПРОФЕССИОНАЛЬНОМУ НАПРАВЛЕНИЮ
Согласно Концепции развития образования Республики
Казахстан (2004-2015гг.) особое
значение приобретает управление качеством образования‚ так как проблемы
качества и его обеспечения замыкают на себя все важнейшие направления реформирования
и модернизация образования. Качество образования представляется в виде составляющих: воспитания и обучения‚
при доминировании последней.
Так как период полного обновления
базового информационного содержания для ряда областей науки и техники
сократился до 3-5 лет‚ приобретаемые в процессе обучения знания уже не могут
выступать в качестве конечной цели обучения. Возникла потребность компонента
более высокого уровня‚ обладающего повышенной устойчивостью по отношению к быстро видоизменяющимся
внешним условиям. Этот компонент состоит из: системного мышления‚ корпоративной
культуры и функциональной грамотности.
Существование конкурентных отношений в сфере
экономики и производства обусловливает действие фактора конкуренции и на рынке
труда, что предусматривает повышение
требований к профессиональной подготовке
специалистов. Резкое ускорение процесса обновления знаний, возникновение новых технологий, непрерывное
техническое переоснащение производства
требуют от специалиста не только качественных знаний, но и высокой профессиональной мобильности, умения
самостоятельно ориентироваться в
обширной научно-технической и экономической информации, постоянно пополнять и обновлять свои
профессиональные знания.
Профессиональная деятельность специальности
информационные
системы это – область науки и техники, которая включает совокупность средств,
способов и методов человеческой деятельности, направленных на создание и
применение систем сбора, передачи, обработки, хранения и накопления информации
[1].
Математика играет важную роль в
естественно-научных, информационно технологических, инженерно-технических и гуманитарных
исследованиях. Она стала для многих отраслей знаний не только орудием
количественного расчета, но также методом точного исследования и средством предельно четкой формулировки
понятий и проблем. Связь математики и естествознания, остоваясь по существу не менее тесной, приобретает
теперь все более сложные формы. Новые теории возникают не только в результате
запросов естествознания и техники, но также и в следствие внутренней
потребности самой математики. Без современной математики с ее
развитым логическим и вычислительным аппаратом был бы невозможен прогресс в
различных областях человеческой деятельности.
Математика – наука о количественных отношениях и пространственных формах
действительного мира. Математика есть орудие познания и изменения природы
человеком. В неразрывной связи с запросами
науки и техники запас количественных отношений и пространственных форм,
изучаемых математикой, непрерывно расширяется [2].
В
математике изучаются математические модели. Это могут быть как
непосредственно математические модели
реальных явлений, так и обьекты (структуры) для изучения этих моделей. Одна и та же математическая модель
может описывать свойства далеких друг от друга по своему конкретному содержанию реальных явлений. Так, одно и то
же дифференциальное уравнение может описывать процессы роста населения и
распада радиактивного вещества. Для математики важна не природа рассматриваемых
обьектов, а существующие между ними отношения.
Рассмотрим пример экономического
характера.
Пример: Обувная мини-фабрика
специализируется по выпуску изделий трех видов: туфли, ботинки и сапоги. При
этом используется сырье трех типов: ![]() .
Нормы расхода каждого из них на одну пару обуви и обьем расхода сырья на один день заданы таблицей:
.
Нормы расхода каждого из них на одну пару обуви и обьем расхода сырья на один день заданы таблицей:
|
Вид сырья |
Нормы расхода сырья на одну
пару,усл.ед. |
Расход сырья на 1 день,усл.ед. |
||
|
туфли |
ботинки |
сопаги |
||
|
|
5 |
2 |
1 |
24 |
|
|
1 |
3 |
2 |
19 |
|
3 |
4 |
3 |
32 |
|
Найти ежедневный обьем выпуска каждого вида обуви.
Решение:Пусть ежедневно фабрика выпускает х
пар туфли, у пар ботинок и z пар сапог. Тогда в соответствии с расходом сырья каждого
вида имеем
систему: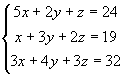
Будем решать
систему уравнение по формулам Крамера.Введем обозначение:
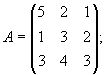
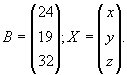
Найдем
определитель системы по правилом треугольников или правилом Сарриюса:
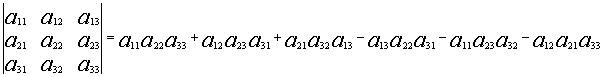
![]()
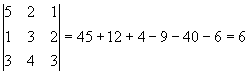
![]() ,
,
Так как ![]() 6
6![]() ,то по теореме Крамера
система имеет единственное решение. Теперь вычислим определители матриц
,то по теореме Крамера
система имеет единственное решение. Теперь вычислим определители матриц ![]() , полученных из матрицы А, заменой соответственно первого, второго и третьего столбцом
свободных членов:
, полученных из матрицы А, заменой соответственно первого, второго и третьего столбцом
свободных членов:
![]() =
=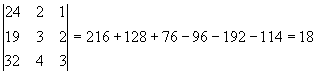
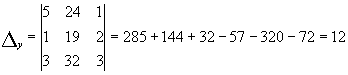
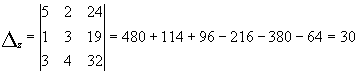 .
.
Теперь по
формулам Крамера:
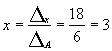 ;
; 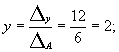 z =
z =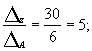
т.е. решение системы уравнений (3;
2; 5). Отсюда можно сделать
слеующий вывод: мини - фабрика
выпускает ежедневно 3 пар туфли, 2 пар ботинок и 5 пар сапог.
В
качестве вывода можно сказать, что в процессе обучения математике студентов специальности
«Информационных систем» важно добиваться наибольшей
рациональности, а не стремиться
сформировать стандартный, одинаковый
для всех стиль, не учитывающий индивидуальных особенностей профессии.
Усвоение учебного материала и формирование индивидуального стиля деятельности
(то есть подготовка к профессиональной деятельности и непрерывному
самообразованию) строятся на основании особенностей позновательных процессов и
способностей.
Литература:
1. Образовательный стандарт специальности (специальность 050703 - «Информационные системы по
отраслям и областям применения)». Южно-Казахстанский
государственный университет им.М.Ауезова,Шымкент-2007г.
2. Бекбоев И.Б.
Научные основы разработки и обучение решению задач в системе математического образования. Дисс.в форме
науч.докл. докт.пед.наук.-Бишкек: 1994.