Технические науки/2. Механика

к.т.н. Мехтиев А.Д., Югай В.В., Эйрих В.И., Белик Г.А.,

Фалалеева О.В.

Карагандинский государственный технический университет, Казахстан

Использование методов компьютерного моделирования для решения проблем надежной эксплуатации механической части тормозного устройства

Актуальность проблемы надежной эксплуатации тормозного устройства (ТУ) шахтной подъемной машины (ШПМ) на протяжении всего срока эксплуатации диктуется нормативными требованиями безопасности, ТУ должно иметь высшую степень надежности. Использование элементов усиления конструкции балки тормозного устройства БТУ ШПМ позволит увеличить ресурс, продлить срок эксплуатации и обеспечить требуемую надежность ТУ. Необходимо разработать многофакторную математическую и имитационную модели, учитывающие все особенности работы БТУ шахтной подъемной машины с целью обеспечения необходимой прочности, повышения ее надежности и увеличения ресурса в процессе эксплуатации. В связи с этим, выбор параметров элементов усиления и разработка методики повышения прочности балки, является актуальной задачей.

В процессе торможения балка передает усилия от пневмоцилиндров через кинематические элементы тормозной системы колодкам, которые взаимодействуют с ободом барабана. Под действием этих усилий балки подвергается изгибающему моменту. Разработана компьютерная математическая модель для анализа и выявления нагруженности элементов тормозного устройства ШПМ 2Ц-4х2,3; 2Ц–5х2,3; 2Ц-5х2,4 и 2Ц-6х2,4, которая позволяет установить зависимости деформации от усилий приложенных к концам балки при изгибающем моменте. Математическая модель позволяет определять зависимость F(x) при Δ= 1…1,34 с учетом разделения балки на слои dx.

Определим деформацию тормозной балки под действием силы приложенной к ее концу. Зависимости силы F от расстояния х до нейтрального слоя при условии, что напряжения в слое балки dx пропорциональны его удлинению, а величина деформации не выходит из зоны пропорциональности. Тогда напряжения на участке l будут иметь вид, показанный на рисунке 1, где х это расстояние от нейтрального слоя до данного слоя dx. Высота балки h=0,4 м, интервал x от 0,2 до 0,4 м с шагом 0,01 м, начальные условия значения приложенной силы на втулку тормозной тяги F=160000 H, F′₀=0, тогда зависимость F(x) установим по выражению:

, МПа (1)

где σ₀ – напряжение в самом удаленном слое от нейтрального, находящемся на расстоянии b от нейтрального, МПа.

Условием будет, что все сечения балки одинаковы и имеют прямоугольную форму, тогда нейтральный слой расположен в середине балки.

, м,

где h – высота поперечного сечения балки, м.

Тогда для тормозной балки шириной сечения α, усилие в слое dx, расположенного на расстояние х, определим по выражению:

, Н. (2)

где σ₀ – напряжение в самом удаленном слое от нейтрального, находящемся на расстоянии b от нейтрального, МПа;

h – высота поперечного сечения балки, м;

α – ширина сечения тормозной балки, м;

Δ – коэффициент усиления конструкции.

Численное исследование модели деформации балки было проведено с помощью лицензионной системы MatLab (Matrix Laboratory), которая является интерактивной системой для выполнения инженерных и научных расчетов, и ориентирована на работу с массивами данных. Для решения систем ОДУ в MatLAB реализованы различные методы. Их реализации названы решателями ОДУ. Решатели реализуют методы решения систем дифференциальных уравнений, «ode45» – одношаговые явные методы Рунге-Кутта 4-го и 5-го порядка.

Рисунок 1 – Расчетная схема

Это классический метод, рекомендуемый для начальной пробы решения. Решим дифференциальное уравнение, вызвав процедуру ode45 из файла-функции txt.1(F,x). Оde45(txt.1, [0.2:0.01:0.4],[160000 0]); решатель ode45, m-файл txt.2, интервал x от 0,2 до 0,4 м с шагом 0,01 м, начальные условия F=160000 H, F’₀=0. Результаты решения математической модели приведены на рисунке 2, для коэффициента усиления конструкции Δ=1 для типовой конструкции без трещин. На рисунке 3 приведены результаты решения модели для Δ=1,34 для конструкции с элементами усиления. Для конструкции, находящейся в эксплуатации в течение 15…25 лет и имеющей усталостные трещины, значение Δ может быть меньше единицы и лежать в пределах 0,5…1. Значение Δ уточняется путем практических измерений НДС с использование средств диагностики.

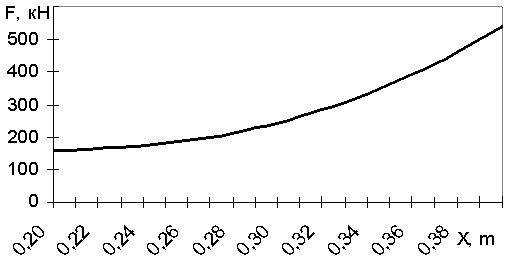
Рисунок 2 – Результаты решения математической модели, зависимость F(x) при Δ= 1

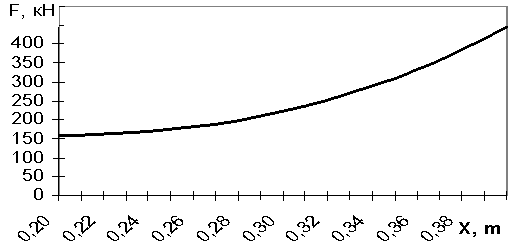
Рисунок 3 – Результаты решения математической модели, зависимость F(x) при Δ= 1,34

Можно сделать вывод о том, что использование элементов усиления позволяет повысить технический уровень конструктивных частей тормозного устройства и обеспечить их нормативную надежность, так как решение математической модели с Δ= 1,34, где конструкция балки, имеет элементы усиления, в отличии от типовой с Δ= 1, способна работать при большем значение силы F, приложенной к ее концу с меньшей деформацией в слое dx и вероятностью развития процессов усталостного разрушения.