Технические науки/4. Транспорт.

Д.т.н. Джиенкулов С.А., к.т.н., Габсаттарова Р.А.

Казахстанский университет «Алатау», Республика Казахстан

Моделирование процесса движения насыпного материала по криволинейному лотку

 

Для оценки правильности проведенных теоретических исследований возникает необходимость проведения экспериментальных испытаний. Одним из методов проведения экспериментальных исследований является применение теории подобия. которая открыла возможность изучать различные технические устройства и физические процессы на моделях.

Сущность моделирования, как метода экспериментальных исследований, заключается в проведении опытов на физической (материальной) модели и распространении результатов на оригинал (натуру). Обычно размеры модели меньше, чем у натуры, что снижает ее стоимость и упрощает испытания, которые могут быть выполнены в лабораторных условиях.

Часто при проведении промышленных (заводских) опытов моделью исследования служит сама промышленная машина (агрегат, установка, комплекс), что облегчает задачу масштабного перехода от модели к оригиналу. Однако в этом случае возможности варьирования параметров процесса ограничены, и моделирование из «активного» становится «пассивным», основываясь лишь на наблюдении и фиксировании значений изучаемых факторов  /1/.

Для правильного использования моделей необходимо четко сформулировать соотношения между параметрами модели и натурной конструкции. Эти соотношения называются законами моделирования или условиями подобия, которые можно получить с помощью принципов подобия.

В технике применяются два больших класса моделей: физические и математические. Физическая модель внешне похожа на натуру, но обычно отличается от нее размерами, может быть выполнена из другого материала и часто работает при механических, тепловых и других воздействиях, отличающихся от натурных. Математическая модель состоит из одного или более уравнений, описывающих поведение изучаемой системы, выведенные из определенных фундаментальных законов и принципов с привлечением упрощающих допущений  /2/. В большинстве случаев моделирование основано на исследовании физически подобных явлений, которое рассматривается как обобщение геометрического подобия, где все геометрические размеры (длина L, ширина B, высота H) подобны, т.е. для модели будет существовать только один масштаб линейных размеров или коэффициент геометрического подобия и все размеры должны быть пересчитаны в соответствии с ним.

Коэффициент геометрического подобия определяется как отношение величины для натуры к величине для модели:

 ,                              (1)

где Lн, Bн, Hн - характерные размеры натуры;

Lм, Bм, Hм - характерные размеры модели.

Существуют и другие масштабы, которые можно определить для каждой переменной величины, характеризующей задачу. Число масштабов, которые можно произвольно назначить равно числу основных размерностей, необходимых для описания переменных. Все другие масштабы можно тогда выразить через эти заданные масштабы.

Критерием подобия называется безразмерный комплекс, величина которого должна быть одинакова для модели и натуры, которые определяются с помощью приведения уравнений процесса к безразмерному виду и с применением «p-теоремы», когда известны параметры, участвующие в процессе  /4/. Важнейшим положением теории размерностей является теорема Бакингема или просто «p-теорема», которая гласит: функциональная зависимость между характеризующими процесс величинами может быть представлена в виде зависимости между составленными из них критериями подобия:

,                                            (2)

где - безразмерные комбинации, составленные из размерных величин, число которых меньше начального числа переменных по отношению к количеству основных размерностей.

Применяя безразмерные комплексы величин, полученные результаты можно распространить на все подобные процессы, уменьшить число величин, которые следует связать функциональной зависимостью.

Необходимые и достаточные условия подобия позволяют выяснить правила перехода от модели к натуре, установить, какие условия следует наложить на системы, чтобы они были подобны. Достаточным условием подобия двух систем является равенство соответствующих критериев подобия этих систем, составленных из их основных параметров и начальных (граничных) условий, т.е.:

       или        .

Получение  p-переменных можно получить следующим образом.

Рассмотрим процесс движения насыпного материала по перегрузочному лотку, спрофилированному по полуарке обыкновенной циклоиды. Скорость движения насыпного материала при  определяется по зависимости:

 ,            (3)

где v0 - начальная скорость движения насыпного материала по лотку, м/с;

g - ускорение свободного падения, м/с2;

Н - высота перегрузки, м;

a - угол, определяющий положение насыпного материала на лотке, град;

k1, k2 - коэффициенты, зависящие от коэффициента трения;

k3 - коэффициент, зависящий от вида кривой, по которой очерчен продольный профиль лотка, и начального положения движения насыпного материала, в данном случае k3 определяется по формуле:

.

Тогда функциональную зависимость скорости движения насыпного материала можно представить в виде:

 .                                       (4)

Т.к.    , а  ,

где v1 - скорость подающего конвейера, м/с;

t - время падения материала с подающего конвейера на лоток, с,

QG - производительность подающего конвейера, т/ч;

q - погонная масса насыпного материала, кг/м3,

то зависимость (4) примет вид:

,                                   (5)

где q; t; H - величины основных единиц измерения.

По «p-теореме» подобия и теории размерностей общее критериальное уравнение скорости движения насыпного материала относительно целевой функции процесса имеет вид (2), в соответствии с которым (5) можно представить:

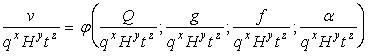.               (6)

Таким образом, отношение (6) представляет собой критерии подобия:

.             (7)

Для первого равенства из (7) получим:

.                                                (8)

Показатели x, y, z определяем из равенства размерностей величин:

,

.

Равенство примет вид:

 ,                                               (9)

где p - критерий подобия, представляющий собой отношение произведения скорости движения насыпного материала и времени к высоте перегрузки.

Аналогичным образом из равенств (7) последовательно получаем:

,

,

,

;                                           (10)

- критерий подобия, характеризующий пропускную способность лотка;

,

,

,

 ;                                          (11)

- критерий, характеризующий ускорение свободного падения;

;

- критерий, характеризующий коэффициент трения;

;

- критерий, характеризующий положение насыпного материала на лотке.

Теперь критериальное уравнение (2) примет вид:

 ,                             (12)

или                              

    .                               (13)

Отсюда видно, что скорость движения насыпного материала по лотку обратно пропорциональна времени и прямо пропорциональна высоте перегрузки, умноженной на функцию критериальных параметров. В итоге создана обобщенная математическая модель процесса движения насыпного материала по криволинейному лотку.

 

Литература:

1.        Седов Л.И. Методы подобия и размерности в механике.-9-е изд., перераб. - М: Наука,1981.- 447 c.

2.        Афанасьева О.В., Голик Е.С., Первухин Д.А. Теория и практика моделирования сложных систем: Учебное пособие. - СПб: СЗТУ, 2005. - 131 с.