МОДЕЛИРОВАНИЕ ВЗАИМОДЕЙСТВИЯ ПОПЕРЕЧНОЙ ДВУХФАЗНОЙ СТРУИ С НАБЕГАЮЩИМ СВЕРХЗВУКОВЫМ ПОТОКОМ

Аманбаев Т.Р., Джумагалиева А., Тилеуов Г.

Южно-Казахстанский государственный университет им. М.Ауезова,

г. Шымкент

Вдув газовых и газокапельных струй в набегающий поток используется для защиты наиболее теплонапряженных элементов энергетических устройств. Взаимодействие газовых струй с набегающими до- и сверхзвуковыми потоками достаточно хорошо исследовано теоретически и экспериментально [1-3]. В то же время влияние дисперсных капель на взаимодействие струй с высокоскоростными потоками изучено недостаточно. Данная работа посвящена численному моделированию поперечного вдува звуковой газокапельной струи из плоского канала (щели) в набегающий вдоль стенки сверхзвуковой поток . Далее параметры набегающего потока газа и вдуваемой струи обозначены нижними индексами “∞” и “j“ соответственно.

Уравнения движения и законы взаимодействия фаз. Примем основные допущения механики многофазных сред [4]. Кроме того, будем полагать, что фазовые превращения отсутствуют, капли сферические (не деформируются), монодисперсные, несжимаемые, между собой не сталкиваются, не дробятся и имеют постоянную теплоемкость. Исследование проводилось в рамках модели невязкого совершенного газа с постоянной теплоемкостью (эффекты вязкости теплопроводности проявляются лишь в процессах взаимодействия газа с каплями). Считалось, что основной поток и вдуваемая струя – один и тот же газ.

В рамках принятых допущений уравнения плоского движения двухфазной газовзвеси капель имеют вид [4]

(1)

(2)

(3)

(4)

, (5)

, , ,

, (6)

, , ; ; .

Здесь нижние индексы 1 и 2 относятся к параметрам несущей и дисперсной фаз; - приведенные и истинные (отмечены верхним индексом 0) плотности, векторы скоростей (u_i , v_i – их компоненты по осям х и у), внутренние и полные энергии, а также температуры и объемные доли газа и капель; - давление газа, газовая постоянная и теплоемкости газа (при постоянном объеме) и капель; n, d – число капель в единице объема смеси и их диаметр; сила аэродинамического взаимодействия между газом и каплей ( - её составляющие по осям х и y) и интенсивность их теплообмена; t - время. Уравнения (1) представляют собой уравнения сохранение масс несущей и дисперсной фаз, уравнения (2) – уравнения сохранения их импульсов, уравнения (4) и (5) – уравнения притока тепла к дисперсной фазе и сохранения полной энергии всей смеси в целом, уравнения (6) – уравнения состояния фаз.

Законы межфазных силового и теплового взаимодействий зададим в форме

, (7)

где С_d - коэффициент аэродинамического сопротивления капли; Nu₁– число Нуссельта; λ₁ – коэффициент теплопроводности газа. Для величин С_d и Nu₁ обычно рекомендуются использовать следующие полуэмпирические соотношения, справедливые для широкого диапазона изменения определяющих параметров [4,5]

(8)

, , ,

, .

Здесь Re₁₂ , Pr₁ и М₁₂ – числа Рейнольдса, Прандтля и Маха; μ₁ и c_p1 –коэффициенты вязкости и теплоемкости (при постоянном давлении) газа; γ и а₁ – показатель адиабаты и местная скорость звука в несущей фазе.

Начальные и граничные условия. Канал, шириной ℓ, располагался перпендикулярно стенке, вдоль которой течет основной поток. Декартовы оси координат выбраны следующим образом: ось x направлена вдоль стенки, ось y – перпендикулярно стенке. В качестве граничных условий на твердых стенках для газа принималось условие непротекания, а для дисперсной фазы (капель) - условие исчезновения из потока. На свободных границах расчетной области принимались следующие условия. На S₁ использовались условия в набегающем потоке, на S₄ – условия вдуваемого газа (рис.1)

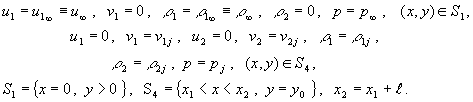(9)

где - координаты (по оси х) левой и правой границ щели; ℓ - ее ширина. На остальных границах S₂ и S₃ принималось условие непрерывности течения. Считалось, что вдуваемая двухфазная газокапельная смесь находится в термодинамическом равновесии ().

В качестве начальных данных задавались соответствующие однородные потоки внутри канала и основной области. Необходимо отметить, что данная постановка начальных условий является упрощенной, так как принятая схема течения в начальный момент времени в действительности не может иметь места. Однако поскольку нас интересует только установившаяся картина течения при , то принятая постановка начальных условий вполне оправдана. В этой связи в данной постановке задачи время фигурирует как параметр установления. Схема задачи, соответствующая начальному моменту времени, показана на рис.1.

В качестве характерной длины задачи использовалась минимальная характерная длина , где и - длины релаксаций скоростей и температур фаз. В качестве характерного времени удобно взять . Характерные длины и вычислялись из выражений [6]

где − характерные числа Маха и Рейнольдса набегающего потока, − скорость звука в нем. В исследованном диапазоне значений определяющих параметров ширина щели всегда была меньше остальных характерных длин, поэтому за величину бралась ширина щели ℓ, а за − характерное время = ℓ / а_{∞ .}

Переход к безразмерным переменным осуществлялся относительно параметров набегающего потока в невозмущенном состоянии

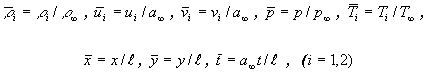
После приведения к безразмерному виду системы уравнений (1)-(6), выражений (7), (8) и граничных условий (9) следует, что критериями подобия процесса взаимодействия газокапельной струи с набегающим потоком будут следующие двенадцать безразмерных величин:

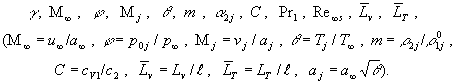
При этом критерий не является существенным, так как исследуется вдув достаточно разреженных взвесей (). Постоянство , а также С, и необходимо для обеспечения подобия течений при наличии межфазного теплообмена. Определяющее влияние на условия течения при взаимодействии двухфазной струи с набегающим потоком обычно оказывают эффекты межфазного трения. Поэтому основными критериями приближенного подобия таких течений можно считать следующие параметры: .

Давление , давление торможения и число Маха струи связаны между собой через газодинамическую функцию давления [7]

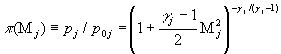
где - показатель адиабаты инжектируемого газа (в связи с принятым здесь допущением она равна показателю адиабаты основного потока ). Приведенная формула необходима для вычисления по заданным и . При этом степень нерасчетности струи k вычисляется по формуле

Отсюда видно, что степень нерасчетности k зависит не только от параметра , но и от числа Маха струи . Параметр φ, характеризующий интенсивность вдува струи, обычно меняется в широком диапазоне (10 ≤ φ ≤ 200) [1].

Некоторые результаты расчетов. Численное моделирование поставленной задачи осуществлялось на основе модифицированного метода крупных частиц [8,9]. Расчеты проводились с помощью алгоритма, разработанного в среде MATLAB. Как известно, алгоритм метода крупных частиц позволяет проводить сквозной счет дифференциальных уравнений (1)-(6) без выделения особенностей типа скачков уплотнения. При этом в расчетах фронт ударной волны занимал не более 2-3 ячеек расчетной сетки. Точность расчетов контролировалась путем повторных пересчетов с уменьшенными вдвое шагами по времени и координатам. Оптимальный шаг счета устанавливался критериями устойчивости и необходимой точности расчета. Расчеты проводились до установления стационарной картины течения.

Ниже обсуждаются результаты расчетов взаимодействия поперечной струи воздуха с каплями воды диаметром d=60 мкм и относительным массовым содержанием m=1, вытекающей из щели при звуковой скорости со сверхзвуковым потоком с числом Маха . Интенсивность вдува φ была равна 16,55 (обычно в экспериментах с поперечным вдувом струй параметр φ меняется от 16 до 212 [1]). При этом степень нерасчетности струи была равна k =8,7. Считалось, что температура вдуваемого газа совпадает с температурой набегающего потока . Расчеты показали, что критические условия, при которых имеет место деформация и дробление капель, во всем поле течения не наступают, так как число Вебера (σ – коэффициент поверхностного натяжения капли), вычисленное по диаметру капель и межфазной скорости, меньше своего критического значения, которое по данным [10] определяется формулой .

Расчеты показали, что перед струей образуется волна уплотнения, фронт которой имеет криволинейную форму. Причем вблизи стенки скачок плотности почти прямой. Анализ показал, что параметры течения за и перед скачком вблизи стенки с большой точностью удовлетворяют соотношениям Ренкина-Гюгонио для прямого скачка. Кроме того, параметры газа в точке полного торможения основного потока перед струей сравнивались со значениями, следующими из интеграла Бернулли. Сравнение показало хорошее согласие расчетных данных с аналитической формулой.

Следует отметить, что в отличие от вдува чисто газовой струи, в случае вдува газокапельной струи на некотором удалении от щели волна уплотнения как-бы разветвляется, принимая «лямбда»-образную форму. Причем вблизи места разветвления перед фронтом волны уплотнения возникает узкая зона сильного разрежения газа. По-видимому, это связано с нагревом газа за счет работы сил трения о межфазную поверхность капель, и последующим его расширением. Еще одна особенность течения, возникающего при вдуве двухфазной газокапельной струи заключается в наличии двух зон разрежения за волной уплотнения. Это объясняется тем, струя вдуваемого газа после выхода из щели почти сразу поворачивает по направлению движения набегающего потока, а «струя» капель по инерции поднимается вверх на значительную высоту, и таким образом, перед набегающим потоком появляются две «преграды», при взаимодействии с которыми возникают две зоны разрежения.

Список литературы

1. Краснов Н.Ф., Кошевой В.М., Калугин В.Т. Аэродинамика отрывных течений.- М.: Высшая школа, 1988, 351 с.

2. Бекетаева А.О., Найманова А.Ж. Численное моделирование сверхзвукового течения с поперечным вдувом струй // Прикладная механика и техническая физика, 2004, т. 45, №3, с.72-80.

3. Глаголев А.И., Зубков А.И., Панов Ю.А. Обтекание струйного газообразного препятствия на пластине сверхзвуковым потоком // Изв. АН СССР. Механика жидкости и газа, 1967, №3, с.97-102.

4. Нигматулин Р.И. Механика многофазных сред.- М.: Наука, 1987, 464 с.

5. Ивандаев А.И., Кутушев А.Г., Нигматулин Р.И. Газовая динамика многофазных сред. - М.: ВИНИТИ, сер. МЖГ, 1981, т. 16, с.209-291.

6. Ивандаев А.И. Об оценке характерных времен динамического и теплового взаимодействия фаз в задачах волновой динамики газовзвесей // Прикладная механика и техническая физика, 1985, №2, с.61-65.

7. Лойцянский Л.Г. Механика жидкости и газа. - М.: Наука, 1987, 840 с.

8. Белоцерковский О.М., Давыдов Ю.М. Метод крупных частиц в газовой динамике. М.: Наука, 1984. 483 с.

9. Губайдуллин А.А., Ивандаев А.И., Нигматулин Р.И. Модифицированный метод крупных частиц для расчета нестационарных волновых процессов в многофазных дисперсных средах // Журнал вычислительной математики и математической физики, 1977, т. 17, №6, с.1017-1027.

10. Гонор А.Л., Ривкинд В.Я. Динамика капли. – М.: ВИНИТИ, сер. МЖГ, 1982, т. 17, с.184-271.