Мельник В.Н., Карачун В.В.
Национальный технический университет Украины «КПИ»
ЛИНЕЙНО-УПРУГИЙ ПОДВЕС ПОПЛАВКОВОГО ГИРОСКОПА
В безразмерной форме
дифференциальные уравнения оболочки с произвольным очертанием линии меридиана
сводятся к виду:
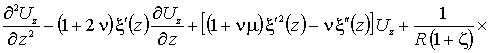


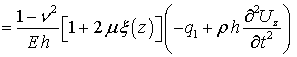 ; (1)
; (1)
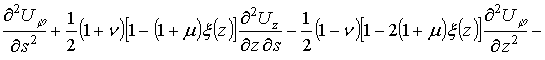
![]()

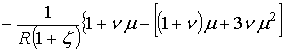
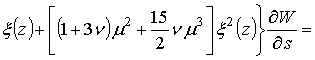
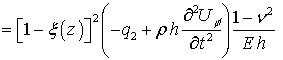 ; (2)
; (2)

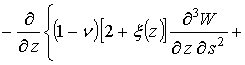
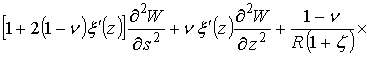
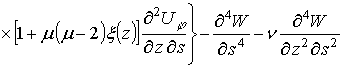
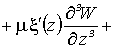

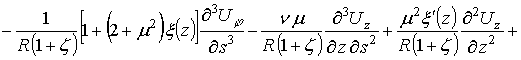


 , (3)
, (3)
где ![]() ,
, ![]() ,
, ![]() – соответственно упругие перемещения
поверхности оболочки вдоль образующей, вдоль параллели, в плоскости шпангоута
(рис. 1);
– соответственно упругие перемещения
поверхности оболочки вдоль образующей, вдоль параллели, в плоскости шпангоута
(рис. 1);
![]() – толщина оболочки;
– толщина оболочки; ![]() – плотность материала;
– плотность материала; ![]() –
модуль Юнга (Young);
–
модуль Юнга (Young); ![]() – коэффициент Пуассона (Poisson);
– коэффициент Пуассона (Poisson); ![]() – радиус по краям;
– радиус по краям; ![]() – длина оболочки;
– длина оболочки; ![]() – расстояние от оси вращения до т. М;
– расстояние от оси вращения до т. М; ![]() – кривая вращения (линия меридиана);
– кривая вращения (линия меридиана);  ;
;  ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() - подъем линии меридиана; при условии, что
- подъем линии меридиана; при условии, что ![]() ,
естественно, что
,
естественно, что ![]() и
и ![]() ;
; ![]() - собственная
частота.
- собственная
частота.
Таким образом, будем
изучать три вида оболочек вращения, т.е. оболочечной части поплавкового
подвеса: выпуклая (рис. 1, а), вогнутая – катеноид, от лат. catena (рис. 1, б), круговой цилиндр (рис. 1, в). Во всех
случаях предполагается, что кривая ![]() ,
образующая оболочку, симметрична относительно линии СМ.
,
образующая оболочку, симметрична относительно линии СМ.
Между системами координат ![]() и
и ![]() имеют место аналитические соотношения –
имеют место аналитические соотношения –
![]() ;
; ![]() .
.
В системе отсчета ![]() линию меридиана зададим выражением
линию меридиана зададим выражением
![]() ,
,
причем знак “+” соответствует
схеме, изображенной на рис. 1, а, а
знак “–” – на рис. 1, б.

Установим класс
кривых ![]() ,
для реализации оболочки. Должны обязательно выполняться условия –
,
для реализации оболочки. Должны обязательно выполняться условия –
![]() ;
;
 .
.
При этом функция ![]() считается строго выпуклой, а функция
считается строго выпуклой, а функция ![]() – строго вогнутой. Функция
– строго вогнутой. Функция ![]() является убывающей при
является убывающей при 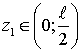 (рис. 1, а) и возрастающей, если
(рис. 1, а) и возрастающей, если  (рис. 1, б). Очевидно, что
(рис. 1, б). Очевидно, что
![]() .
.