Математика/4.Прикладная математика

К. ф.‑м. н. Карнаух Т.А.

КНУ им. Т. Шевченко, Украина

Иерархии вычислимых чисел и функций

По аналогии с временной и емкостной иерархиями языков [1] можно рассматривать аналогичные иерархии вычислимых действительных чисел и вычислимых действительных функций. Действительное число x вычислимо, если его двоичное представление w=a_m…a₀Ña_-1…ÎD¢=({0}È È1{0,1,2}^*)Ñ{0,1,2}^wÈ({0}È{0,,}^*)Ñ{0,,}^w (a_iÎ{0,1,2,,}, символы , понимаются как "минус 1" и "минус 2", Ñ – как запятая; ||||= -1, ||||= -2, x=||a_m…a₀Ña_-1…||=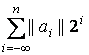) может быть вычислено машиной Тьюринга, работающей на выходной ленте в режиме дописывания символов в конец выходного слова [2]. Если при этом для выдачи первых n символов на выход требуется не более чем f(n) единиц времени (рабочей памяти) для всех nÎN, то говорим, что число вычислимо со временем (на памяти) f(n).

Продолжая аналогию, если на каждом входе из множества D=D¢Ç Ç{0,1,,Ñ}^w и представляющем число из области определения действительной функции g, соответствующая машина Тьюринга (R-преобразователь, [3]) для получения n символов результата использует не более чем f(n) единиц времени (рабочей памяти) для всех nÎN, то говорим, что функция g вычислима со временем (на памяти) f(n).

Общеизвестно, что все рациональные числа вычислимы за линейное время на константной памяти. Очевидным представляется также и то, что функции g(x,y)=x+y и g(x,y)=x-y вычислимы на памяти O(n) за время O(n). Путем перенесения алгоритмов длинной арифметики, использующих рекуррентные соотношения, на бесконечные представления действительных чисел получаем, что функции g(x,y)=x×y, g(x)=1/x, g(x)=x^k, kÎN, вычислимы на памяти O(n) за время O(n²).

Теорема 1. Если все числа a_i вычислимы на памяти f(n) со временем g(n), то функция p(x) = a₀+a₁x¹+...+a_mx^m, D_f = [‑1, 1], вычислима на памяти O(max{f(n), n}) за время O(max{g(n), n²}).

Доказательство. Для заданных a_i сначала вычислим наименьшее kÎN такое, что для всех i выполнено |a_i|£2^k. Для всех i произведение a_ixⁱ может быть вычислено на памяти O(max{f(n), n}) со временем O(max{g(n), n²}). Поскольку |a_ixⁱ|£2^k при xÎD_f, то сумму полученных произведений можно вычислить на конечной памяти за линейное время. Следовательно, значение p(x) может быть вычислено на памяти O(max{f(n), n}) за время O(max{g(n), n²}).

Следствие 1. Любое алгебраическое число вычислимо на памяти O(n) за время O(n²).

Доказательство. Алгебраическое число x можно представить в виде x = 2^k×y, где kÎN, |y| £ 1. Без ограничения общности можно считать, что y является корнем уравнения p(x) = 0, где p(x) = a₀+a₁x¹+...+a_mx^m, a_iÎQ (iÎ) и p(x) не имеет кратных корней. Функция p(x), D_f  = [‑1, 1], вычислима на памяти O(n), поэтому y можно вычислить методом половинного деления на памяти O(n) за время O(n²). Умножение на 2^k сводится к переносу запятой, что завершает доказательство.

Следствие 2. Любое вычислимое число, не вычислимое на памяти O(n) или за время O(n²), является трансцендентным.

Теорема 2. Если функция p(x) = a₀+a₁x¹+...+a_mx^m, D_f = [‑1, 1], a_m ¹ 0, вычислима на памяти (со временем) f(n), то a₀ вычислимо на памяти (со временем) f(n), а числа a_i (iÎ) вычислимы на памяти (со временем) O(f(n)).

Доказательство. Очевидно, что a₀ = p(0). Остальные коэффициенты получим как решение системы a₁2^-i+...+a_m2^-mi = p_i = p(2^-i)-p(0), iÎ. При этом a_i можно представить в виде a_i = p₁×(A_i,1/D)+…+p_m×(A_i,m/D), где D – детерминант системы, A_i,j – соответствующие алгебраические дополнения, не зависящие от p_j. Рациональные числа A_i,j/D не зависят от полинома p, а числа p_i вычислимы на памяти (со временем) O(f(n)). Из последнего следует, что a_i вычислимо на памяти (со временем) O(f(n)).

Теорема 3. Для любой рекурсивной функции f(n) существует вычислимое число, которое не вычислимо на памяти (со временем) f(n).

Доказательство. Пусть LÍ1{0,1}* – произвольный рекурсивный язык, N_L={||v|| | vÎL}, a_i = 01 при iÎN_L, и a_i = 00 при iÏN_L, w = 0Ña₀a₁…, x = ||w||. Предположим, что число x вычислимо на памяти f(n). Учитывая структуру его записи без переполнения, любая его запись с переполнением может быть приведена к записи без переполнения путем задержки результата на два знака. Таким образом, будем постепенно вычислять число x, вычитая при этом единицу из входного слова на каждые два выходных символа дробной части. Тогда для вычисления a_i нам потребуется O(f(2i+2)+i) памяти (и O(f(2i+2)+i2ⁱ) времени). То есть всякий рекурсивный язык разрешим на памяти O(f(2n+2)+n) (со временем O(f(2n+2)+n×2ⁿ)). Противоречие.

Следствие 3. Для любой рекурсивной функции f(n) существует полином p(x) = a₀+a₁x₁+...+a_mx^m, D_f = [‑1, 1], с вычислимыми коэффициентами, который не вычислим на памяти (со временем) f(n).

Литература:

1. Hopcroft J.E., Ullman J.D. Introduction to automata theory, languages and computation. Addison-Wesley Publishing Company, 1979, 418 p.

2. Карнаух Т.О. Обчислюваність трансцендентних чисел генераторами з гніздовою стековою пам'яттю. // Вісник Київського університету. Серія: фізико-математичні науки. - 2003. - № 3. - С. 216-220.

3. Лисовик Л.П. Алгоритмические вопросы для реальных функций. // Кибернетика. – 1987. – № 1. – С. 12-17.

e-mail: tkarnaukh@unicyb.kiev.ua