Кусмухамбетов М.Е., Бакирбаев Б.
Республика Казахстан, Теразский
Государственный Университет
им. М.Х. Дулати, г. Тараз
Республика Казахстан, Таразский
Педагогический институт, г. Тараз
Оценка экологической обстановки на
основе использования численных моделей
В данной
работе, на основе использования численной модели для оценки экологической
обстановки источников вредных примесей, рассматриваются примеры нахождения
параметров выбросов для ряда производств промышленного города. Рассматривается
пример снижения мощности выбросов за счет использования определенной комбинации
перевода ряда промышленных предприятий со старого вида топлива на новое
топливо.
Сформулируем следующую
оптимизационную задачу [1]:
Найти вектор ![]()
![]() Е, доставляющий
минимум суммарной функции стоимости:
Е, доставляющий
минимум суммарной функции стоимости:
![]()
![]()
![]() (1)
(1)
при ограничениях
![]()
![]() (2)
(2)
Здесь ![]() - средняя концентрация примеси за определенный промежуток
времени в точке
- средняя концентрация примеси за определенный промежуток
времени в точке ![]() при уменьшении
мощности источников на вектор
при уменьшении
мощности источников на вектор ![]() R – предельно допустимая концентрация
примеси в области D; Е={
R – предельно допустимая концентрация
примеси в области D; Е={![]()
![]() }.
}.
Для определения поля концентрации,
создаваемого i-м источником единичной мощности ![]() , воспользуемся уравнением [2,3]:
, воспользуемся уравнением [2,3]:
![]() (3)
(3)
с граничными и начальным условиями
![]() при z=0;
при z=0; ![]() =0 при z=H;
=0 при z=H;
(4)
![]() ;
; ![]()
где ![]() - вектор скорости ветра;
- вектор скорости ветра; ![]() ;
; ![]() ,
, ![]() - коэффициенты
горизонтальной и вертикальной турбулентности; Р,
- коэффициенты
горизонтальной и вертикальной турбулентности; Р,![]() - заданные функции;
- заданные функции;
S – граница области D; ![]() ) – функция, описывающая расположение i-го источника и режим его функционирования во времени;
) – функция, описывающая расположение i-го источника и режим его функционирования во времени; ![]() ,
, ![]() - операторы дивергенции и градиента функции в горизонтальных
направлениях.
- операторы дивергенции и градиента функции в горизонтальных
направлениях.
В силу
линейности задачи (3),(4) суммарное поле концентрации ![]() , создаваемое всеми источниками, определится выражением:
, создаваемое всеми источниками, определится выражением:
![]() (5)
(5)
где ![]() - фоновое поле концентрации, создаваемое нерегулируемыми
источниками,
- фоновое поле концентрации, создаваемое нерегулируемыми
источниками, 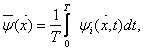
![]() .
.
Подставляя
выражение (5) в(2), получим задачу математического программирования:
![]()
![]()
![]() (6)
(6)
![]()
![]() (7)
(7)
Если функция ![]() неубывающие, для решения задачи (6),(7) могут использоваться
методы выпуклого программирования [4].
неубывающие, для решения задачи (6),(7) могут использоваться
методы выпуклого программирования [4].
Рассмотрим сначала задачу по
определению минимального количества нового топлива, требующего для замены
старого, с целью достижения допустимого уровня концентрации примеси №3 на исследуемой
территории.
Выбросы примесей №3 происходят из 29
источников. В настоящее время осуществляется перевод предприятий на более
качественное топливо. Однако его не всегда достаточно, и поэтому предприятия
вынуждены иногда использовать старое топливо.
В результате расчета поля концентрации в 17
точках сеточной области при существующем выбросе получилось превышения ПДК.
Задача минимализации имеет вид:
![]()
![]()
![]() (8)
(8)
![]()
![]()
![]()
![]()
![]() (9)
(9)
Функции Gi (ei) здесь линейны и определяются через
разницу в стоимости старого и нового топлива.
Обратимся
теперь к случаю, когда поступление нового топлива ограничено. Попытаемся
наиболее рациональным способом распределять имеющиеся в наличие количество
этого топлива между предприятиями.
Возможную оптимизационную постановку запишем как набор задач с минимизацией
функционала вида:
![]()
![]() (10)
(10)
при ограничениях
![]()
![]()
![]() (11)
(11)
где ![]() – количество нового
топлива, имеющееся на энергетических предприятиях,
– количество нового
топлива, имеющееся на энергетических предприятиях, ![]() – коэффициент,
определяющий количество нового топлива, в результате сжигания которого (в замен
старого) выброс в атмосферу примеси №3 снижается на 1 усл.
ед. Решение задачи (10),(11) проводилось для следующих значений
– коэффициент,
определяющий количество нового топлива, в результате сжигания которого (в замен
старого) выброс в атмосферу примеси №3 снижается на 1 усл.
ед. Решение задачи (10),(11) проводилось для следующих значений ![]() :
: ![]()
![]()
![]() Здесь
Здесь ![]()
![]() - решение задачи
(3),(4). Результаты расчетов приводятся в табл. 1
- решение задачи
(3),(4). Результаты расчетов приводятся в табл. 1
Наиболее интересным из результатов,
на взгляд авторов, представляется пример, связанный с оптимизацией выбросов
примесей №3 приведенный в таблице 1. Из таблицы 1 следует, что для достижения ПДК достаточно
перевести на новое топливо 12 предприятий из 29, причем в число подлежащих
регулированию попали в основном источники, имеющие сравнительно небольшие
мощности выброса.
Таблица 1
|
Источник |
Относительное снижение примеси №3, усл. ед. |
|||
|
Задача 1 |
V1 |
V2 |
V3 |
|
|
10 |
1 |
0,8 |
1 |
1 |
|
13 |
1 |
0 |
1 |
1 |
|
14 |
1 |
0 |
1 |
1 |
|
15 |
1 |
0 |
0 |
0 |
|
18 |
1 |
0 |
0 |
1 |
|
19 |
1 |
0 |
0,25 |
1 |
|
20 |
0,44 |
0 |
0 |
1 |
|
21 |
1 |
0 |
1 |
1 |
|
22 |
1 |
0 |
1 |
1 |
|
23 |
1 |
0 |
0 |
0 |
|
24 |
1 |
0 |
0 |
0 |
|
25 |
1 |
0 |
0 |
0,5 |
Литература
1. Пененко В.В. Некоторые модели оптимизации
режима работы источников загрязнения атмосферы //Метеорология и гидрология. –
1983. - №2. – с. 59-68.
2. Марчук Г.И. Математическое
моделирование в проблеме окружающей среды. - М .: Наука, 1982.
3. Берлянд М.Е. Современные проблемы
атмосферной диффузии и загрязнения атмосферы. – Л.:Гидрометеоиздат,
1975.
4. Еремин И.И., Астафьев Н.Н. Введение в
теорию линейного и выпуклого программирования. – М.: Наука, 1976.