УДК 621.762 (669.721)

Пестова Г.С.

Восточно-Казахстанский государственный технический университет

Моделирование  процесса  гранулирования 

металлических  расплавов

Известно много способов получения гранулированных материалов [1], выбор схемы гранулирования предопределяется крупностью, формой и назначением, а также физико-химическими характеристиками гранул. для получения гранул из агрессивных расплавов металлов и сплавов выбран метод диспергирования расплава самораспадом струи, или метод свободного слива расплава: струя сама разбивается на капли без дополнительного воздействия на струю [2]. Этот метод характеризуют удобное и простое аппаратурное оформление процесса, небольшие скорости течения расплава, отсутствие источников загрязнения гранул, применимость для расплавов разной плотности и теплоемкости.

Для промышленного получения гранул необходимо оптимизировать:

- режим диспергирования с учетом химического состава расплава;

- режим охлаждения с учетом тепловой нагрузки расплава и характеристик охлаждающей среды или холодильника-кристаллизатора.

Цель настоящей работы – разработка на основе современных представлений диспергирования [3] математической модели, алгоритм которой прогнозирует и управляет  процессом получения гранулы определенного размера из металлического расплава заданного химического состава.

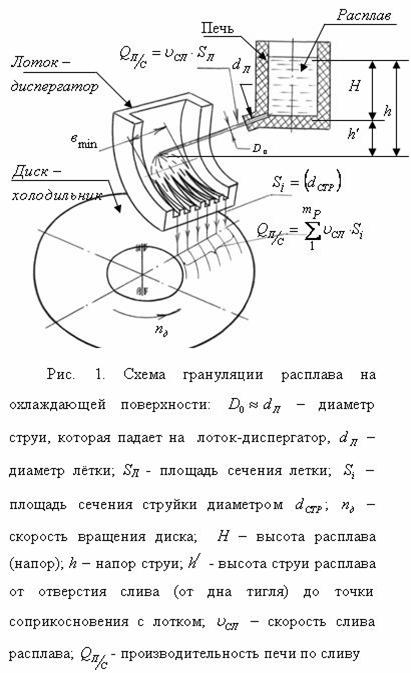
Некоторые моменты математического моделирования процесса самораспада струи металлического расплава. Прежде всего, диспергирование расплава самораспадом реализуется формированием струек, которые будут распадаться во время свободного падения. С этой целью расплав сливают на многоручьевой лоток-диспергатор (рис.1), в котором струя за счет центробежных сил преобразуется в плоскую струю «», затем делится на число руьёв-струек «» сечением определенного диаметра  [2].

Уравнение для определения ширины плоской струи  «» связывает параметры  плавильной печи, расплава и струи:

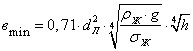, мм                                                                        (1)

где  – плотность расплава, кг/м3; – поверхностное натяжение, Н/м; h – высота струи, м;  - диаметр струи, которая падает на лоток-диспергатор;  – диаметр лётки печи, м; .

для струек исследуемого интервала диаметров = 1÷10 мм, выполняется расчёт числа ручьёв слива :

,                                                                                                         (2)

откуда на один ручей слива будет приходиться часть площади плоской струи расплава , разделённой  на количество ручьёв  :

,                                                                      (3)

где  – площадь сечения отверстия слива (лётки);  – площадь сечения струйки для ;  – сечение ручья слива, при  этом диаметр  должен находиться в интервале диаметров самораспада. при этих условиях  принимается эквивалентным сечению струйки диаметром .

известно, что основным параметром диспергирования расплава материала самораспадом при свободном сливе является объёмный расход: объём образующейся капли, равный объёму отрезка цилиндрической струйки длиной . Характеристиками диспергирования струи, и параметрами модели, обеспечивающими основной параметр, являются: скорость истечения расплава , диаметр струи расплава или диаметр самораспада струи , длина нераспавшейся части струи L.

растущая амплитуда максимальной волны становится контуром будущей капли, а длина этой волны зависит от диаметра струи  и определяет размер капли.      

так как скорость истечения при самораспаде определяется высотой напора расплава h, в интервале  справедлива формула Бернулли: , где μ − коэффициент расхода.

Величину «L» рассчитывают по формуле задаваясь значениями

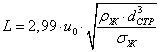                                                                                      (4)

в координатах  , по расчетным значениям «L» для диаметра струи  в интервале  скоростей ,  строится номограмма  зависимости длины L струи  расплава от скорости истечения   при  для ряда диаметров отверстия истечения.

Если провести на номограмме линию параллельно горизонтальной оси на минимальном или заданном расстоянии «L», она пересечёт графики  в определённых точках. Координаты этих точек и определяют сочетания значений скорости  истечения  и диаметра струи расплава , при  которых распад струи расплава будет происходить  на расстоянии  не менее «Lmin» от отверстия истечения.

Отмеченные математические зависимости были использованы в разработке алгоритма (рис.2) компьютерной модели для расчета параметров технологии диспергирования струи расплава самораспадом. первоначально модель протестировали на расплаве фторида бериллия, используя данные экспериментальных исследований диспергирования расплава фторида бериллия [2].

Заключение

● Разработана математическая модель для расчета диспергирования агрессивных расплавов металлов и сплавов самораспадом струи.

● модель позволяет определять и прогнозировать технологические (высота струи, температура расплава, диаметр капли) и конструктивные (лоток-диспергатор и его размеры, расстояние до охлаждающей среды) параметры установки. первоначально модель проверена на расплаве фторида бериллия.

 

Список литературы

1. Новое в технологии получения материалов /А.И. Манохин, А.М. Поживанов, К.А. Блинов и др. Под ред. Ю.А. Осипьяна, А.Хауффа. – М.: Машиностроение; Ханау: Лейболд АГ, 1990. – 448 с.

2. Пестова Г.С. Моделирование процесса и разработка технологии грануляции расплава фторида бериллия. Кандидатская диссертация, Алматы. 2006 г.

3. Силаев А.Ф., Фишман Б.Д. диспергирование жидких металлов и сплавов. – М.: Металлургия, 1983, 144 с.