УДК 621.01.

Иванова А. П.^*, Штыцко П.И.^**

*Национальная металлургическая академия Украины,** Днепропетровский национальный технический университет железнодорожного транспорта им. академика В.А.Лазаряна

Определение положения линии контакта на поверхности зуба косозубой рейки.

Развитие исследований в области расчетов прочности зубьев косозубых колес требуют уточнения некоторых вопросов теории зубчатого зацепления. Так, например, при исследовании напряженного состояния зуба косозубой рейки возникает необходимость точно определить положение линии контакта на боковой поверхности зуба.

В работах Ф.Л.Литвина [1] и В.А.Гавриленко [2] подробно рассматриваются общие вопросы зацепления косозубых колес. Однако приводимые ими формулы не удобны для практического использования, по ним достаточно сложно определить положение линии контакта зубьев.

Ю.Н.Бунаков [3] проводит формулу для определения линии контакта, полагая, что рабочая поверхность косого зуба представляет собой прямоугольник.

В предлагаемой работе показано, что эта поверхность аа´bb´ (рис.1) представляет собой не прямоугольник (как считает Ю.Н.Бунаков), а параллелограмм. На рисунке 1 сечение mnb₀´b´ проведено перпендикулярно оси зуба. Следовательно,

, . (1)

Из треугольников оmk, оb´k и mb´k получаем

, (2)

где β – угол наклона зуба;

α_n – угол зацепления в нормальном сечении зуба.

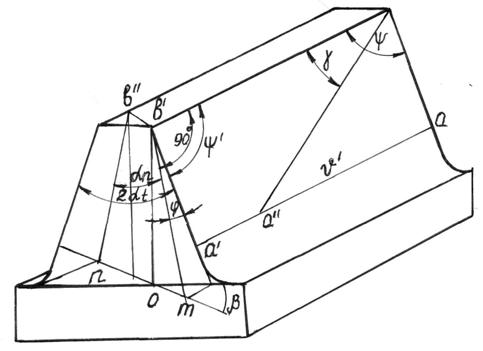
Рис.1. Рабочая поверхность косого зуба

Рассмотрим зацепление косозубой рейки с зубчатым колесом (рис.2).

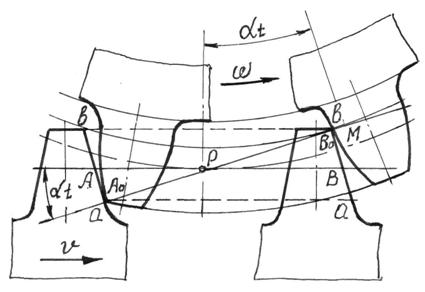
Рис. 2.Зацепление косозубой рейки с колесом

Принимаем рейку ведущей. Зуб рейки входит в зацепление в точке а. далее линия контакта под углом γ (угол между кромкой зуба и линией контакта) перемещается по боковой поверхности зуба в пределах контура аа´bb´. Из треугольника аа´´b получаем.

, (3)

где - длина рабочего участка линии зацепления;

- ширина рабочего участка зуба рейки в осевом направлении.

Из треугольника aab (рис.2) определяем

, (4)

где - длина рабочего участка линии зацепления ;

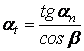- угол зацепления в торцевом сечении.

Скорость перемещения линии контакта в направлении (рис.1 и рис. 3) определяем по формуле

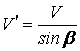, (5)

где - поступательная скорость рейки.

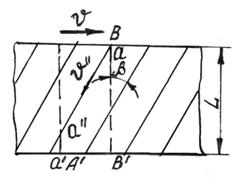
Рис. 3. Скорость перемещения линии контакта V^’ в направлении аа

Длина отрезка ,

где – время прохождения зубом реки отрезка (рис.2), следовательно

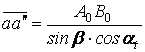. (6)

Подставляя выражения (4) и (6) в формулу (3) получаем:

. (7)

Используя (1), (2) и (7) определяем угол между кромкой зуба косозубой рейки и линией контакта.

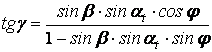. (8)

В таблице 1 приведены значения углов γ, расчитаные для нескольких значений углов β [4].

Таблица 1

β	8º	10 º	12 º	14 º	16 º	18 º	20 º
γ	2 º30´	3 º27´	4 º0´	4 º53´	5 º30´	6 º17´	7 º0´

Литература:

1.Литвин. Ф. Л. Теория зубчатых зацеплений. М.: Наука, 1968- 584 с.

2.Теория механизмов. Под. ред. Гавриленко В.А М.: Высшая школа, 1973 - 510 с.

3.Бунаков Ю. Н. О линии контакта косозубых и шевронных колес. Сб. Теория механизмов и машин. Из-во Харьковского университета, 1967.-С.27 -35.

4.Андреев В. И. Справочник конструктора машиностроителя, Т.2, М.: Машиностроение, 1980 -56 с.