Южаков И.Ю., Филиппова Т.С.
Карагандинский
государственный технический университет, Казахстан
Зависимость минимального габаритного размера планетарного механизма
кинематического варианта А от передаточного отношения
В многоступенчатых
передачах и в редукторах общее передаточное отношение разбивается по ступеням
(частным передаточным отношениям). Универсальных рекомендаций по разбивке,
удовлетворяющих всем основным условиям не существует. На практике часто
разбивку общего передаточного отношения производят из условия удовлетворения
главного критерия, зависящего от вида передачи и от назначения рабочей машины.
Для сложных передач,
применяемых в горных машинах, в частности приводах очистных и проходческих
комбайнов, таким критерием является требование минимизации высоты редуктора для
вписывания в ограниченное пространство, получения одинакового погружения в
масляную ванну и создания наименьшей установочной площади корпуса редуктора.
Используя разработанный в
[1] методический подход, проанализируем влияние основных размеров на габариты
планетарных механизмов.
Рассмотрим планетарный
механизм кинематического варианта ![]() с цилиндрическими
колесами. Наибольшее влияние на габариты этого вида механизмов оказывает радиус
расположения осей сателлитов –
с цилиндрическими
колесами. Наибольшее влияние на габариты этого вида механизмов оказывает радиус
расположения осей сателлитов – ![]() .
.
Из
кинематической схемы механизма (рис. 1) видно, что продольный и поперечный
размеры совпадают по величине ![]() .
.
Определим ![]() :
: ![]() . Из формулы
. Из формулы ![]() , находим
, находим ![]() . Из условия сносности находим
. Из условия сносности находим ![]() и
и ![]() . Зная
. Зная ![]() и
и ![]() , находим
, находим ![]()
![]() .
.
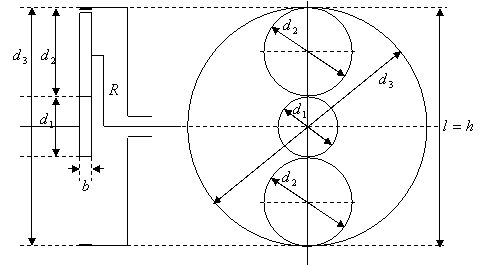
Рис.1 Планетарный механизм кинематического варианта А.
Далее найдем ![]() . Воспользуемся формулой, используемой при проектном расчете
прочности [2]
. Воспользуемся формулой, используемой при проектном расчете
прочности [2]
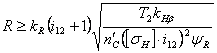 (1)
(1)
где ![]() - вспомогательный
коэффициент,
- вспомогательный
коэффициент, ![]() ;
; ![]() - передаточные числа
- передаточные числа ![]() ;
; ![]() - крутящий момент,
действующий на большее колесо рассчитываемой пары;
- крутящий момент,
действующий на большее колесо рассчитываемой пары; ![]() - коэффициент,
учитывающий неравномерность распределения нагрузки по длине зуба;
- коэффициент,
учитывающий неравномерность распределения нагрузки по длине зуба; ![]() - приведенные числа
сателлитов
- приведенные числа
сателлитов ![]() , где
, где ![]() - число установленных
сателлитов;
- число установленных
сателлитов; ![]() - допускаемое
контактное напряжение;
- допускаемое
контактное напряжение; ![]() - коэффициент ширины
зубчатого колеса.
- коэффициент ширины
зубчатого колеса.
Возводим значение формулы
(1) в куб и перегруппируем входящие в нее члены
![]() .
.
Левая часть неравенства
характеризует несущую способность передачи в зависимости от ее основных
параметров и называется геометрическим показателем несущей способности передачи
![]() (2)
(2)
Правая часть неравенства
определяется нагрузкой и допускаемым напряжением и ее обозначают ![]()
![]() .
.
Очевидно при проектном
расчете ![]() .
.
Решив (2) относительно ![]() , получим
, получим
 (3)
(3)
Принимая ![]() за постоянную
величину, проанализируем зависимость
за постоянную
величину, проанализируем зависимость ![]() от
от ![]() и
и ![]() . При заданном
. При заданном ![]() зависимость
зависимость ![]() от
от ![]()
 , где
, где ![]() .
.
Исследуем
эту функцию на минимум в интервале ![]()
![]() .
.
Откуда ![]() . После подстановки
. После подстановки ![]() , получаем
, получаем
![]() , при
, при ![]() .
.

Рис.2
График изменения ![]() от
от ![]() и
и ![]()
Используя полученные
зависимости, построим график изменения ![]() от
от ![]() и
и ![]() (Рис. 2).
(Рис. 2).
Из графика видно, что
передаточные отношения существенно влияют на основной размер ![]() . Выполненный анализ соответствует случаю, когда величина
. Выполненный анализ соответствует случаю, когда величина ![]() задана и,
следовательно, крутящий момент на колесе остается постоянным. Из графика так же
следует, что незначительное отклонение передаточного отношения вызывает не
существенное изменение основного размера
задана и,
следовательно, крутящий момент на колесе остается постоянным. Из графика так же
следует, что незначительное отклонение передаточного отношения вызывает не
существенное изменение основного размера ![]() .
.
Таким образом, радиус
расположения осей сателлитов ![]() , соответствующий передаточному числу, может быть определен
аналитически формула (3), либо графически (Рис. 2).
, соответствующий передаточному числу, может быть определен
аналитически формула (3), либо графически (Рис. 2).
Литература:
1. Н.Я. Ниберг. Расчет редукторов. Выбор
параметров и табличный метод расчета передач. - М.: Машиностроение, 1964.
2. А.В. Кузьмин и др. Расчеты деталей
машин: Справочное пособие/А.В. Кузьмин, И.М. Чернин, Б.С. Казинцов. – 3-е
издание, перераб. и дополн. – Минск, Высшая школа, 1986.