Иванова А. П., Каряченко Н. В.

Национальная металлургическая академия Украины

ЭКВИВАЛЕНТНЫЕ НАПРЯЖЕНИЯ ПРИ ПЛОСКОМ НАПРЯЖЕННОМ СОСТОЯНИИ УПРУГО - ПЛАСТИЧЕСКИХ МАТЕРИАЛОВ

Введение. Третья и четвертая теории прочности, применяемые при изучении напряженного состояния упруго – пластических материалов, основаны на предположении, что причиной появления пластических деформаций в материале являются большие касательные напряжения, и эти деформации никак не связаны с упругим изменением объема. Известно, что во всех случаях напряженного состояния материала (кроме чистого сдвига), наибольшие касательные напряжения действуют во взаимодействии с нормальными. В результате чего появляются упруго - пластические деформации и связанное с ними изменение объема и формы тела. В свою очередь, изменение объема материала влияет на процесс возникновения и развития деформаций [1, 2] - то есть получается взаимосвязанный процесс.

Постановка задачи. В предложенной работе рассмотрена попытка принимать за критерий опасного состояния упруго - пластических материалов полное напряжение в площадках наибольшего сдвига, которое учитывает взаимодействие сдвига и отрыва частиц материала. При этом два напряженных состояния можно считать эквивалентными по прочности, если полные напряжения на площадках наибольшего сдвига одинаковы.

Результаты. В практике расчетов различают три вида напряженного состояния (рис. 1):

1) объемное – действуют три главных напряжения (σ1, σ2 ,σ3);

2) плоское – действуют два главных напряжения (третье равно нулю);

3) линейное – действует одно главное напряжение ( два главных напряжения  равны нулю).

Нумерация главных напряжений устанавливается таким образом, чтобы σ1 обозначало наибольшее по абсолютной величине напряжение, а σ3 -  наименьшее [2]. При исследовании напряженного состояния элементов конструкций чаще встречается плоское ( двухосное ) напряженное состояние.

Рисунок 1 – Напряженно – деформированное состояние

                    элементарного параллелепипеда

 

 При плоском напряженном состоянии  можно записать:

                 (1)

где  - полное напряжения.

При линейном растяжении до предела текучести :

,                                                     (2)

где  - предел текучести.

Условие состояния текучести материала будет иметь вид:

                                                              (3)

Выражение (3) справедливо для идеально равнопрочных материалов, работающих на растяжение и сжатие, поэтому знаки главных напряжений в нем не учитываются. Это условие может быть использовано для всех случаев плоского напряженного состояния материала, когдя знаки нормальных напряжений в опасных сечениях не влияют на результаты расчетов.

Условие прочности для плоского состояния на основании выражения (3) принимает вид:

                                                           (4)

Если главные напряжения  , то , тогда:

,                    (5)

Подставив значения главных напряжений (5) в выражение (4) получим условие прочности в таком виде:

 .                                      (6)

Используем это условие для расчета круглого вала при совместном действии изгиба с кручением, когда  .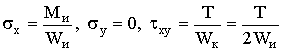

Получим

,               (7)

где Т- скручивающий момент.

Для изгиба с кручением получим:

,   ,                     (8)

где:

 Q – сила, изгибающая вал,

А – площадь поперечного сечения вала.

                    (9)

При МИ = 0 получим  для растяжения с кручением:

,                                   (10)

где  F – сила, растягивающая вал.                                                                       

Пользуясь условием (3) определим соотношение между пределами текучести по нормальным и касательным напряжениям. Для чистого сдвига

; , откуда ,      (11)

что совпадает со справочными данными для сталей средней и повышенной прочности [4] .

Далее получим выражение для определения n - коэффициента запаса прочности стального вала по пределу текучести при одновременном действии нормальных и касательных напряжений. За основу принимаем выражения (6) и (11), предлагаемого способа определения прочности :

 ,          (12)

где: 

 - коэффициент запаса прочности по нормальным напряжениям;

 - коэффициент запаса прочности по касательным напряжениям .

Пример. Используя предлагаемую методику, выполним расчет по третьей  и четвертой  теориям прочности представленной на рисунке 2 консольной балки, если известно: =1 м, F=0,5 кН, Т=0,85 кН·м, балка выполнена из Ст. 5, [σ] = 150 МПа, σТ =290 МПа.

Рисунок 2 – Консольная балка

 

  кН·м

 МПа,

где

м3 – момент сопротивления  при изгибе в сечении I – I.

 МПа ,

где  м3 –  момент сопротивления при кручении в сечении

I –I, [4].

,

,

.

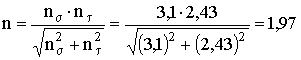Расчетные значения этих же величин сотавляют:

- по третьей теории прочности : Мэкв =0,986 кН·м , d = 41 мм, σа=73,93 МПа, Wи=6,763·10-6 м3, τа=70,42 МПа, Wк, нетто=12,07·10-6 м3, nσ = 3,92, nτ = 2,92, n = 2,34;

- по четвертой теории прочности: Мэкв =0,89 кН·м , d = 40 мм, σа=79,62 МПа, Wи=6,28·10-6 м3, τа=72,09 МПа, Wк, нетто=12,07·10-6 м3, nσ = 3,64, nτ = 2,86, n = 2,25.

Выводы. Предлагаемая методика определения прочности материалов, в отличие от  III и IV теорий прочности, позволяет уменьшить расчетные размеры детали, что ведет к экономии материалов. В то же время значения коэффициента запаса прочности, полученные при расчете консольной балки на изгиб с кручением по предлагаемой методике и по III и IV теориям прочности достаточно близки. Это подтверждается приведенным примером.

 

 

Литература:

1. Афанасьев А. М., Марьин В.А. Лабораторный практикум по сопротивлению материалов. – М.: Наука, 1975. – 287 с.

2. Писаренко Г. С., Агарев В.А. и др. Сопротивление материалов. Киев: Вища школа, 1986. – 195 с.

3. Прочность, устойчивость, колебания. Справочник Т. 1.,под ред. Биргера И. А., Пановко Я. Г. - М.: Машиностроение, 1968 – 831 с.

4. Анурьев В.И. Прочность, устойчивость, колебания. Справочник Т.– М.: Машиностроение, 1980 –728 с.