Экономические науки/

8. Математические методы в экономике

Осипенко Н.Н., к. т. н. Баранов А.Н.

Донбасский государственный технический университет

Оптимизация инвестиционного портфеля коммерческого банка

Рассмотрим процесс оптимизации портфеля коммерческого банка с точки зрения получения стабильного дохода. Для решения данной задачи предлагается сформировать портфель с заданной ожидаемой доходностью.

В классической теории оптимизации портфеля ценных бумаг [1] предполагается формирование портфеля из n-видов ценных бумаг, произвольно взятых на рынке.

В нашем подходе предлагается первоначально производить качественную оценку ценной бумаги и составление рейтинга. Оценка производится на основе следующих параметров, которым будет присвоен коэффициент в диапазоне от 0 до 1: определение страны, в которой выпускается акция (уровень развития страны); определение отрасли (коэффициенты для стран по отраслям предполагаются разные, в зависимости от вклада данной отрасли в ВВП страны); определение класса эмитента согласно законодательства [2]; расчет относительного прироста прибыли компании на одну акций; расчет относительного прироста дивидендов на одну акцию; сравнение текущего уровня доходности с ожидаемым уровнем; сравнение совокупной доходности акции с ожидаемым уровнем; сравнение текущей доходности со ставкой банковского процента.

На основе полученного рейтинга в портфель будут включаться первые десять акций, потому что согласно принципу диверсификации и осуществленным ранее исследованиям ученными включения большего количества акций не имеет смысла.

Допустим, нужно сформировать портфель с заданной ожидаемой доходностью .

Для определения возможного ожидаемого уровня доходности воспользуемся концепцией модели рынка в соответствии, с которой доходность портфеля, составленного из обращающихся на рынке акций, определяется характеристиками рыночного портфеля и будет записана формулой [3]:

(1)

где ожидаемая доходность (портфеля, акции);

коэффициенты регрессии.

доходность рыночного портфеля (акции).

Для нахождения коэффициентов регрессии применяем МНК.

Доходность рыночного портфеля рассчитывается как отношение суммы удельного веса капитализации фирмы на доходность акции и суммы удельного веса всех акций.

Рассчитав ожидаемую доходность портфеля, можем более обосновано определить какой ожидаемый уровень нам выбрать.

Решение задачи с заданной ожидаемой доходностью вытекает из решения общей задачи максимизации функции полезности инвестора.

Функция полезности инвестора, характеризующая его отношение к доходности и риску записывается следующим уравнением:

(2)

где параметр предпочтения между риском и доходностью.

ожидаемая доходность портфеля;

стандартное отклонение ожидаемой доходности портфеля.

Ожидаемая доходность портфеля рассчитывается по формуле:

(3)

где доля i-той ценной бумаге в портфеле (i=1,2,…,n);

ожидаемая доходность i-той ценной бумаги.

Стандартное отклонение ожидаемой доходности рассчитывается по формуле:

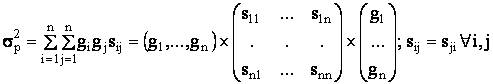(4)

где доля i-той ценной бумаге в портфеле (i=1,2,…,n);

ковариация между i-той и j-той ценными бумагами.

Основываясь на модели рынка, ожидаемая доходность i-той ценной бумаги определяется доходностью рыночного портфеля и может быть рассчитана с помощью формулы (1). Согласно модели рынка доходность акции представляется в виде двух компонент: и . Коэффициент является степенью риска акции относительно степени риска рыночного портфеля: при , риск данной акции больше, чем рыночного портфеля, при – риск данной акции меньше риска рыночного портфеля. Определив коэффициент , можно отсеять рискованные бумаги с портфеля, которые не были определены при рейтинговой оценке.

Максимизация функции полезности запишется как:

(5)

.

Воспользуемся функцией Лагранжа и запишем условие максимизации в матричном виде:

(6)

Уменьшаемое обозначим , первый множитель вычитаемого – С, второй множитель вычитаемого – .

Тогда условие максимизации Лагранжа можно записать в виде:

(7)

Определим обратную матрицу к матрице С. Обозначим все ее элементы, кроме последнего столбца и строки, . Элементы последнего столбца и последней строки получаются одинаковыми, и их обозначим , где ,, .

Для определения оптимальной структуры портфеля остается решить систему уравнений:

(8)

Обозначим , получим следующую формулу для расчета оптимальной доли каждого вида ценных бумаг в портфеле:

(9)

Определим портфель с минимальным риском. Параметр представляет собой тангенс угла, образованного осью ординат и касательной к области выбора инвестора в точке, соответствующей оптимальному портфелю. Когда инвестор отдает предпочтение портфелю с минимальным риском, тогда касательная становится параллельно оси ординат, поэтому . Следовательно, у такого портфеля , то есть последний столбец (строка) обратной матрицы представляет структуру портфеля с минимальным риском. Доходность и риск его будут равны: ,

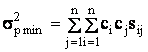
Для определения структуры портфеля, отвечающего другим требованиям инвестора, удобно использовать специфический показатель:

(10)

Используя показатели  , , легко можно найти структуру портфеля, соответствующего конкретным требованиям инвестора.

Теперь мы можем сформировать портфель с заданной ожидаемой доходностью :

(11)

Из равенства (11) определим, какому значению соответствует желание инвестора иметь ожидаемую доходность портфеля, равную :

(12)

Подставив значение , полученное из выражения (12), в уравнение (9), найдем структуру портфеля с заданной ожидаемой доходностью:

(13)

Таким образом, будет получен портфель позволяющий, получить фиксированный уровень дохода, который соизмерим с общей динамикой на рынке ценных бумаг.

Литература:

1. ШАРП, Уильям Ф.Инвестиции: Пер. с англ./У.Ф. Шарп, Д.В. Бэйли,

Г. Дж. Александер. – М.:ИНФРА-М, 2001. – 1027с.

2. Постанова правління національного банку України від 17.12.2003

№ 561. Про затвердження Положення про порядок визначення справедливої вартості та зменшення корисності цінних паперів.

3. Тарасевич Л.С., Гребенников П.И., Леусский А.И. Макроэкономика: Учебник. — 6_е изд., испр. и доп. — М.: Высшее образование, 2006. — 654 с.