К.И. Юренко, Е.И. Фандеев, Ю.А. Жлоба

ЮРГПУ(НПИ) им. М.И. Платова, г. Новочеркасск

Программный комплекс для МАтеМАТИЧЕСКОГО

моделирования движения поезда

Повышение энергоэффективности, безопасности и надежности функционирования железнодорожного транспорта в условиях увеличения интенсивности грузопотока, организации скоростного и высокоскоростного движения во многом связано с повышением уровня автоматизации систем управления, что позволяет оптимизировать процесс движения поездов и уменьшить влияние человеческого фактора.

Совершенствование бортовых систем управления и автоведения является одной из актуальных задач для достижения указанной цели. Оно позволит облегчить труд локомотивных бригад и персонала депо, повысить точность исполнения расписания и снизить расход электроэнергии и топливных ресурсов в условиях динамически изменяющихся фактов внешней среды, таких как изменение графика движения поездов в режиме реального времени, поездной обстановки, напряжения в контактной сети и параметров основного сопротивления движению, связанных с техническим состоянием подвижного состава и железнодорожной инфраструктуры, погодными условиями и др.

Одним из основных методов исследования и оптимизации таких систем с учётом большого числа факторов и сложности их описания является математическое моделирование с использованием высокопроизводительных средств вычислительной техники. Для этого авторами разработан специализированный программный комплекс. При программировании использовалась среда Microsoft Visual C++ 2008 Express Edition, поддерживающая объектно-ориентированную методологию разработки программного обеспечения (ПО).

Структура компьютерной модели представлена на рис. 1 и включает в себя следующие основные модули, реализованные в виде классов на языке С++. Модель тяговой системы в качестве исходных данных использует тяговые, а также характеристики электрического торможения локомотива и зависимость к.п.д. от скорости.

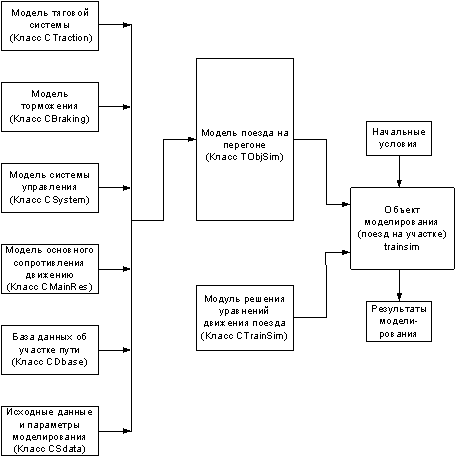
Рис. 1 – Структура программного комплекса

Модель торможения позволяет моделировать процесс электропневматического торможения поезда, а модель системы управления - реализует алгоритмы управления тягой, электрическим и электропневматическим торможением, функцию регулятора скорости, ограничения ускорения при разгоне и замедления при торможении. В качестве исходных параметров задаются значения скорости стабилизации на различных участках движения, координаты перехода на выбег и скорость начала торможения, от выбора которых зависит время хода и расход электроэнергии. При заданном времени хода задача оптимизации заключается в оптимальном распределении времени хода по перегону и выборе указанных выше параметров. Модель основного сопротивления движению основана на эмпирической зависимости его значения от скорости и позволяет задавать коэффициенты, определяющие отклонение фактических параметров сопротивления от расчётных с учетом таких дополнительных факторов, как ветер и пониженная температура окружающей среды (от минус 25 ºС и ниже) [1]. База данных об участке пути содержит: ограничения скорости, профиль и кривизна пути, а также координаты станций и светофоров. Исходные данные включают координаты начала и конца участка моделирования, число вагонов, их загрузку и заданное время хода.

Модель поезда на перегоне объединяет все перечисленные модели в единую структуру, на основе которой создается программный объект «поезд на участке» и с помощью модуля решения уравнений движения осуществляется процесс моделирования.

На основе известного основного уравнения движения [1] c учетом: специфики локомотивов, оборудованных автоматизированным тяговым приводом с непрерывным регулированием сил тяги и электрического торможения, а также системой автоведения; представления поезда как гибкой нерастяжимой нити; влияния ветра и пониженной температуры, предлагается следующая форма записи уравнения:

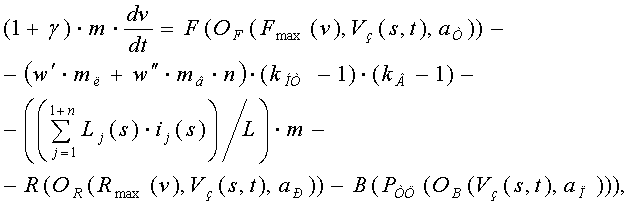
где , , ,– скорость, текущее время и пройденный путь соответственно; – коэффициент инерции вращающихся частей; и – массы локомотива и средняя масса вагона с учётом загрузки; – число вагонов; и – удельное основное сопротивление движению локомотива и вагона; , – коэффициенты, учитывающие пониженную температуру воздуха и наличие ветра; – длина поезда; – участок пути, занимаемый поездом; – удельное дополнительное сопротивление движению поезда от уклонов и кривых пути, воздействующее на часть поезда, находящуюся на участке;, , – силы тяги, электродинамического и пневматического торможения; , , – операторы, моделирующие работу системы управления; , - максимально возможные силы тяги и электрического торможения при текущей скорости движения, определяемые тяговыми и тормозными характеристиками тягового привода; - давление в тормозных цилиндрах; - скорость, заданная системой автоведения в текущий момент времени; - ускорение, заданное в режиме тяги; , замедления в режиме электрического и пневматического торможения соответственно.

Блок-схема алгоритма моделирования представлена на рис. 2. После ввода исходных параметров (координаты начала и конца участка, а также число вагонов) осуществляется чтение базы данных, затем в цикле осуществляется моделирование работы системы управления и подсистем локомотива (тяговой, тормозной), а также расчёт основного и дополнительного сопротивления движению. После этого рассчитывается удельная ускоряющая сила как отношение суммы сил, действующих на поезд (правая часть приведенного уравнения движения) к массе поезда. Затем решаются управления движения поезда, определяются его путь и скорость в каждый момент времени и далее рассчитывается расход электроэнергии – суммарный , на тягу и её возврат в процессе рекуперативного торможения . Более подробно методика моделирования описана в [2-5]. Время расчёта движения поезда на участке 15 км на персональном компьютере составляет несколько секунд. Математическая модель и реализующее её ПО позволяют исследовать различные программы движения и законы регулирования, реализуемые системой управления (регулятор скорости, подсистема управления пневматическими тормозами и др.) с целью поиска оптимальных с точки зрения расхода электроэнергии на тягу управления при различных условиях движения.

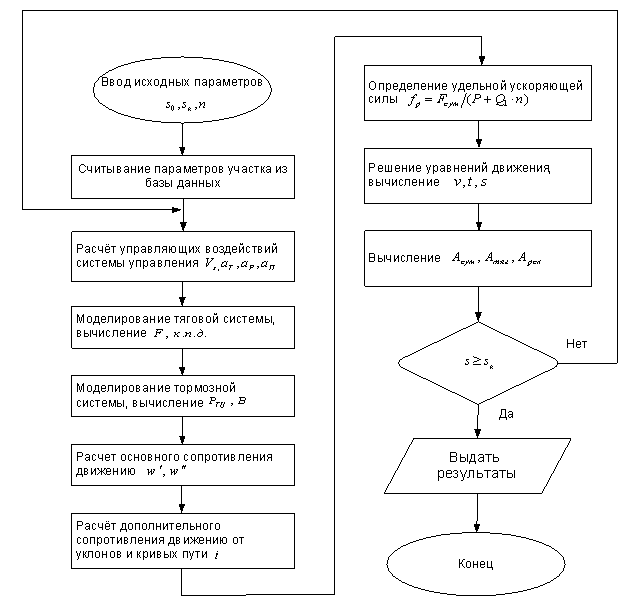
Рис. 2 - Блок-схема алгоритма моделирования

Для конкретного перегона может быть различными способами (численным, аналитически, численно-аналитическим) осуществлен выбор основных параметров траектории (ускорение и замедление, скорости стабилизации на различных участках, точка перехода на выбег, скорость начала торможения) и выполнен вычислительный эксперимент для получения оценки данной траектории (расход энергии, среднее значение к.п.д., дисперсия скорости и др.).

В качестве примера использования модели найдем оптимальные траектории движения поездом на участке длинной 15 км при встречном, попутном ветре и при его отсутствии. Расчётные траектории представлены на рис. 3, а численные результаты вычислительных экспериментов сведены в табл. 1.

Таблица 1 – Численные результаты вычислительных экспериментов

№ №	Скорость стабилизации, км/ч	Координата начала выбега, км	Замедление в режиме рекуперативного торможения, м/с	Наличие ветра	Время хода, с	Расход энергии (суммарно/ на тягу/ возврат при рекуперации), кВт·ч
1	118	9.100	0.2	нет	600 ± 2	382/480/98
2	120	9.000		встречный 10 м/с		423/514/91
3	115	9.850		попутный 10 м/с		346/455/109

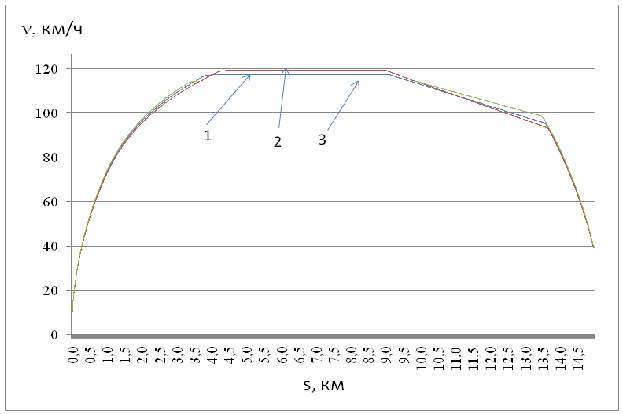
Рис. 3 – Результаты вычислительных экспериментов по поиску оптимальных траекторий движения: 1 – без ветра, 2 – встречный и 3 – попутный ветер

Таким образом, описанный в статье программный комплекс для исследования математической модели движения поезда может быть использован для определения оптимальных программ движения поездов, оптимизации траекторий движения на основе вычислительного эксперимента, а также прогнозирования расхода электроэнергии при различных неконтролируемых факторов внешней среды, таких как наличие ветра и пониженной температуры окружающей среды. Из приведенных данных видно, что наличие ветра может оказывать существенное влияние на оптимальную траекторию движения поезда и расход энергии.

Литература:

1. Осипов, С.И. Теория электрической тяги: Учебник для вузов ж.-д. транспорта / С.И. Осипов, С.С. Осипов, В.П. Феоктистов // Под. ред. С.И. Осипова. – М.: Маршрут, 2006. – 436 с.

2. Юренко, К.И. Аппаратно-программный комплекс для моделирования и автоматизированного управления движением поезда / К.И. Юренко, Е.И. Фандеев // Известия вузов. Северо-Кавказский регион. Технические науки. 2012, № 2. – С. 26-31.

3. Юренко, К.И. Компьютерная модель и программно-аппаратные средства бортовой системы автоматизированного ведения поезда / К.И. Юренко, Е.И. Фандеев // Известия ЮФУ. Технические науки. 2012, №5. – С.51-56.

4. Юренко, К.И. Расчёт энергооптимальных режимов движения перспективного подвижного состава методом динамического программирования / К.И. Юренко // Известия вузов. Электромеханика. 2013, №3. – С. 78-82.

5. Юренко, К.И. Автоматизация исследований энергооптимальных режимов ведения поездов / К.И. Юренко // Вестник Восточно-украинского национального университета им. В. Даля. Техн. науки. Серия Транспорт. Луганск: 2013, №18(207). Ч.2 – С.109-113.